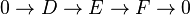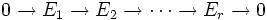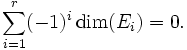Théorème du rang - Définition

Introduction

En mathématiques, le théorème du rang de l'algèbre linéaire, lie le rang et la dimension du noyau d'une application linéaire. Soient E et F deux espaces vectoriels sur un corps K et soit une application linéaire. Alors

,

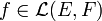
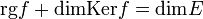
où rgf désigne la dimension de l'image de f.

Pour démontrer le théorème, on vérifie que pour toute base du noyau et toute base de l'image, est une base de E. En effet, cette famille est génératrice (pour tout vecteur x, en notant x_t les coordonnées de f(x) dans la base de l'image et x_s celles de dans la base du noyau on obtient ) et libre (sous l'hypothèse , on obtient, en prenant l'image par f, , donc par indépendance des f(v_t) les b_t sont nuls, si bien que l'hypothèse de départ se simplifie en , dont on déduit, par indépendance des u_s, que les a_s sont nuls aussi).

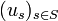
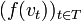
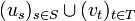
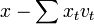
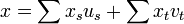
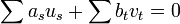
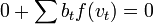
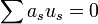
Cas particulier des endomorphismes

Soit f une application linéaire d'un espace vectoriel E dans lui-même. On a la relation:

.

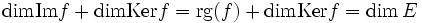
Autres formulations et généralisations

Ce théorème est une forme du premier théorème d'isomorphisme de l'algèbre dans le cas des espaces vectoriels.

Dans un langage plus moderne, le théorème peut être énoncé de la manière suivante : si

est une suite exacte courte d'espaces vectoriels, alors

dim(D) + dim(F) = dim(E)

Ici F joue le rôle de Imf et D celui de Kerf.

En dimension finie, cette formulation peut être généralisée : si

est une suite exacte d'espaces vectoriels de dimension finie, alors

Le théorème du rang pour des espaces vectoriels de dimension finie peut aussi être formulé en termes d'indice d'application linéaire. L'indice d'une application linéaire , où E et F sont des espaces vectoriels de dimension finie, est défini par

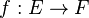
indicef = dim(Kerf) − dim(Cokerf) où Coker désigne le conoyau de f.

Intuitivement, Kerf est le nombre de solutions indépendantes x de l'équation f(x) = 0, et dim(Cokerf) est le nombre de restrictions indépendantes qui doivent être mises à la place de y pour rendre l'équation f(x) = y résoluble. Le théorème du rang pour des espaces vectoriels de dimension finie est équivalent à la proposition

indicef = dim(E) − dim(F)

Nous voyons que nous pouvons facilement déterminer l'indice d'une application linéaire f à partir des espaces impliqués, sans nul besoin d'étudier f en détail. Cela se remarque également dans un résultat beaucoup plus profond : le théorème de l'indice d'Atiyah-Singer qui affirme que l'indice de certains opérateurs différentiels peut être obtenu à partir de la géométrie des espaces impliqués.

v · d · m Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Famille génératrice • Famille libre (indépendance linéaire) • Base • Théorème de la base incomplète • Rang • Colinéarité
Sous-espace	Sous-espace vectoriel • Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Diagonalisation • Endomorphisme nilpotent
En dimension finie	Espace vectoriel de dimension finie • Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford • Décomposition de Frobenius
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau