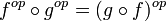Théorie des catégories - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Une catégorie

- d'une classe dont les éléments sont appelés objets,
- d'un ensemble
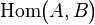
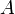
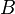
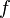
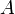
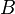
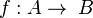
- d'un morphisme
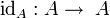
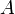
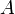
- d'un morphisme
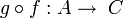
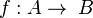
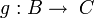
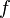
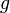
-
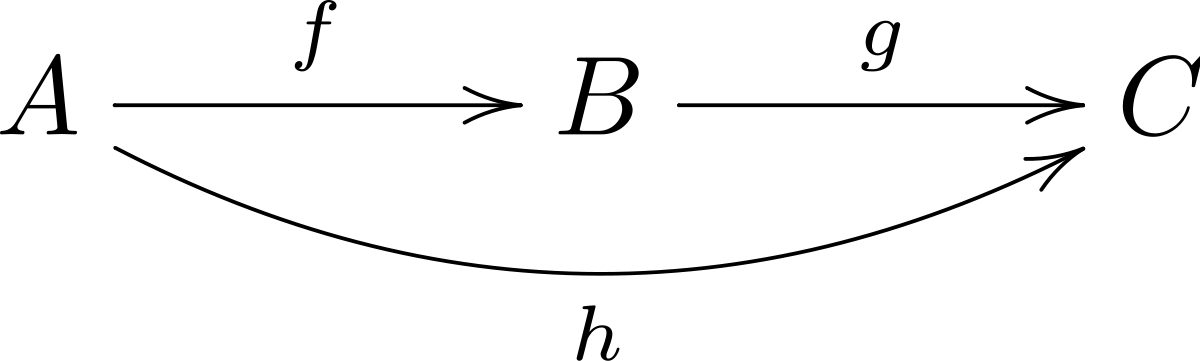
- la composition est associative : pour tous morphismes
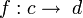
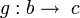
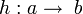
-
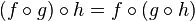
- les identités sont des éléments neutres de la composition : pour tout morphisme
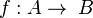
-
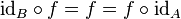
- la composition est associative : pour tous morphismes
On demande aussi que :
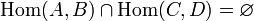
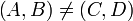
Lorsqu'une catégorie est courante, certains lui donnent comme nom l'abréviation du nom de ses objets, entre parenthèses, pour signaler qu'il s'agit de leur catégorie ; nous suivrons ici cette convention.
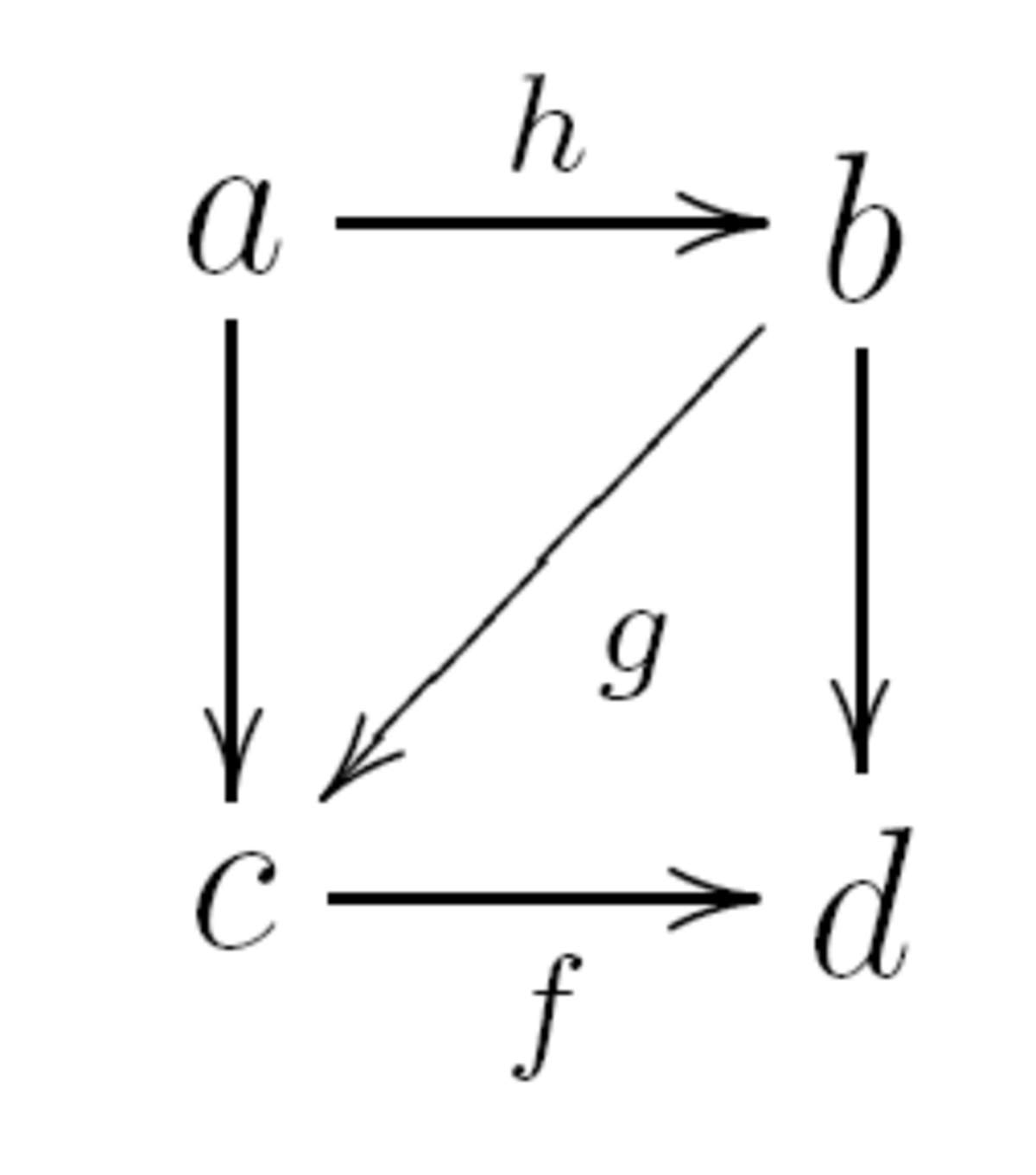
Une sous-catégorie de



Propriétés des flèches
Définitions
Une flèche
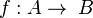
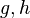
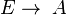

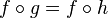
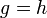
Une flèche
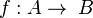
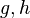
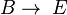

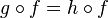
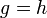
Les notions de monomorphisme et d'épimorphisme sont duales l'une de l'autre : une flèche est un monomorphisme si et seulement si elle est un épimorphisme dans la catégorie duale.
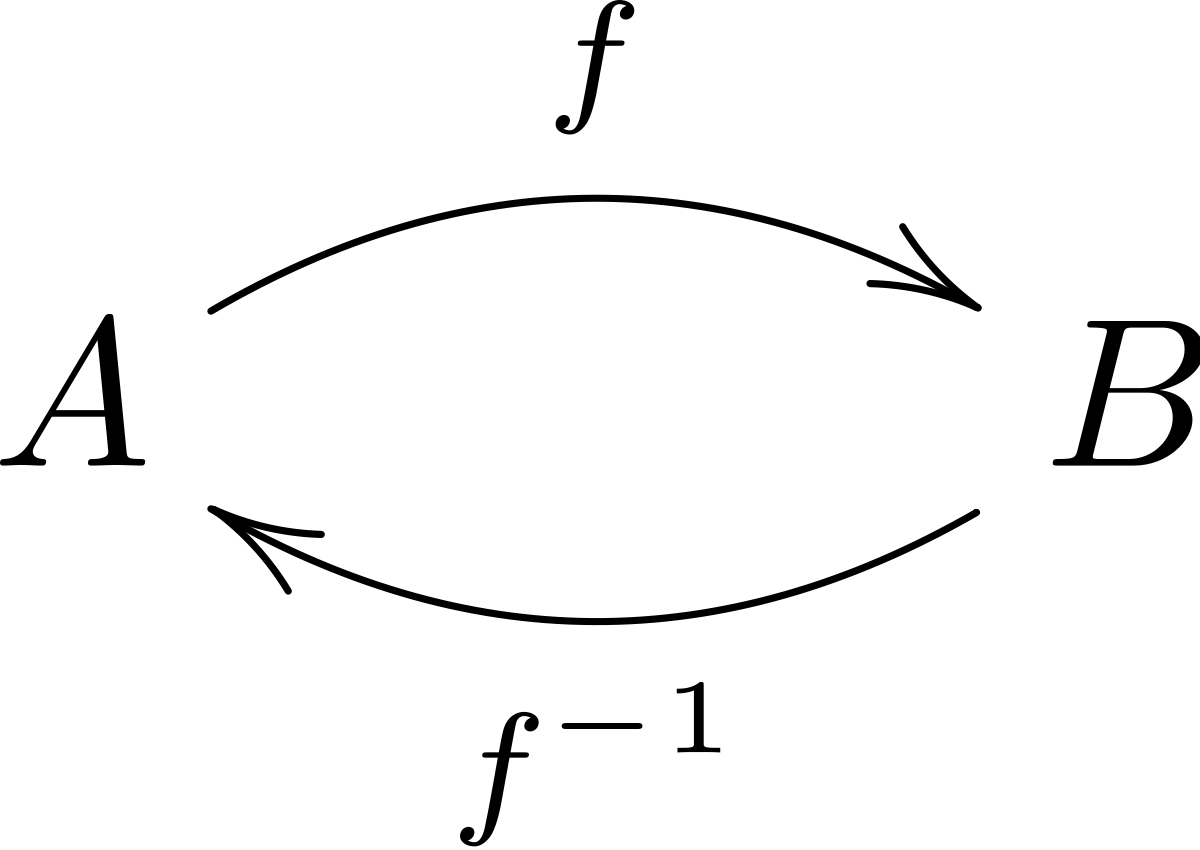
Une flèche
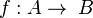
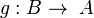
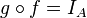
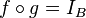
Exemples
- Dans la catégorie des ensembles, les monomorphismes sont les injections, les épimorphismes sont les surjections et les isomorphismes sont les bijections.
- Un contre-exemple important en théorie des catégories : un morphisme peut à la fois être un monomorphisme et un épimorphisme, sans être pour autant un isomorphisme ; pour voir ce contre-exemple, il faut se placer dans la catégorie des anneaux commutatifs unitaires, et considérer la flèche (unique!)
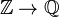
- On trouve aussi de tels épimorphisme-monomorphisme non-isomorphiques dans la catégories des espaces topologiques : toute injection y est un monomorphisme, toute surjection est un épimorphisme, les isomorphismes sont les homéomorphismes, mais il y a des fonctions continues à la fois injectives et surjectives qui ne sont pas des homéomorphismes : par exemple l'identité sur un ensemble muni de deux topologies différentes, l'une plus grossière que l'autre.
- Dans la catégorie des ensembles ordonnés les isomorphismes sont les bijections croissantes (elles sont nécessairement strictement croissantes).
Catégorie duale
À partir d'une catégorie

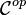
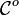
Plus précisément :
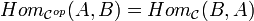
Il est clair que la catégorie duale de la catégorie duale est la catégorie de départ :
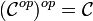
Cette dualisation extrêmement simple permet de symétriser la plupart des énoncés, ce qui peut être douloureux pour les débutants...