Théorie des catégories - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie des catégories étudie les structures mathématiques et les relations qu'elles entretiennent.
Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l'informatique théorique et en mathématiques de la physique. Elles forment une notion unificatrice. Cette théorie a été mise en place par Samuel Eilenberg et Saunders Mac Lane en 1942-1945, en lien avec la topologie algébrique et propagée dans les années 1960-70 en France par Alexandre Grothendieck qui en fit une étude systématique.
Éléments de base
L'étude des catégories, très abstraite, fut motivée par l'abondance de caractéristiques communes à diverses classes liées à des structures mathématiques.
Voici un exemple. La classe Grp des groupes comprend tous les objets ayant une « structure de groupe ». Plus précisément, Grp comprend tous les ensembles G muni d'une relation binaire qui satisfait un certain ensemble d'axiomes. Des théorèmes peuvent ainsi être prouvés en effectuant des déductions logiques à partir de cet ensemble d'axiomes. Par exemple, ils apportent la preuve directe que l'élément identité d'un groupe est unique.
Au lieu d'étudier simplement l'objet seul (les groupes) qui possède une structure donnée, comme les théories mathématiques l'ont toujours fait, la théorie des catégories met l'accent sur les morphismes et les processus qui préservent la structure entre deux objets. Il apparaît qu'en étudiant ces morphismes l'on est capable d'en apprendre plus sur la structure des objets.
Dans notre exemple, les morphismes étudiés sont les homomorphismes de groupes. Un homomorphisme de groupe entre deux groupes préserve la structure de groupe d'une manière très précise ; c'est un processus qui à un groupe en associe un autre, tout en préservant toutes les informations sur la structure du premier groupe au sein du second groupe. L'étude des homomorphismes de groupe fournit alors un outil pour étudier les propriétés générales des groupes et les conséquences des axiomes relatifs aux groupes.
Il en est de même dans de nombreuses théories mathématiques. Une catégorie est une formulation axiomatique qui relie des structures mathématiques aux fonctions qui les préservent. Une étude systématique des catégories permet de prouver des résultats généraux à partir des axiomes d'une catégorie.
Une catégorie est elle-même un type de structure mathématique, pour laquelle il existe des processus préservant sa structure. De tels processus sont appelés foncteurs.
Exemples
- La catégorie
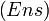
- La catégorie
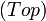
- La catégorie
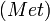
- La catégorie
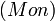
- La catégorie
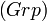
- La catégorie
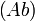
- La catégorie
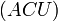
- La catégorie
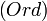
Les exemples précédents ont une propriété en commun : les objets sont des ensembles munis d'une structure supplémentaire, et les flèches sont toujours des applications entre les ensembles sous-jacents. Ce sont des catégories concrètes, c'est-à-dire des catégories munies d'un foncteur fidèle vers la catégorie des ensembles (dans les cas présents, il s'agit de foncteur oubli). Cette propriété est très particulière. Voici des exemples de catégories sans cette propriété :
- On se donne un monoïde
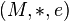

-
- objets : un seul
- flèches : les éléments du monoïde, elles partent toute de l'unique objet pour y revenir ;
- composition : donnée par la loi du monoïde (l'identité est donc la flèche associée à

- On se donne un ensemble

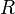
-
- objets : les éléments de l'ensemble ;
- flèches : pour tous objets




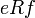
- composition : la composée de deux flèches est la seule flèche qui réunit les deux extrémités (la relation est transitive) ; l'identité est la seule flèche qui relie un objet à lui-même (la relation est réflexive).
- Cet exemple est particulièrement intéressant dans le cas suivant : l'ensemble est l'ensemble des ouverts d'un espace topologique, et la relation est l'inclusion ; cela permet de définir les notions de préfaisceau et de faisceau, via les foncteurs.

















































