Contre-exemple - Définition

Introduction

En mathématiques, un contre-exemple est un exemple, un cas particulier ou un résultat général, qui contredit les premières impressions. Un contre-exemple peut aussi être donné pour rejeter une conjecture, c'est-à-dire un énoncé que les gens (et en particulier les mathématiciens) pensaient vrai.

Négation d'une généralité

La recherche d'un contre-exemple est une méthode utilisée pour prouver que certaines affirmations, prétendant à un certain caractère de généralité (i.e. les propositions universelles), sont fausses. Quand un énoncé commence par «  Pour tout .... », il suffit, pour prouver qu'il est faux, de trouver un élément (« il existe ... ») qui réalise les conditions imposées dans l'hypothèse sans que ne soit vérifiée la conclusion. C'est la donnée du contre-exemple.

Contrairement à la vie courante, où il est d'usage de dire que l'exception confirme la règle, en mathématique, l'existence d'une exception infirme la règle.

Cette méthode est utilisée très tôt dans la pratique mathématique soit pour mettre à bas une conjecture, soit pour prouver qu'une propriété n'est pas réalisée.

Ainsi pour prouver qu'une fonction réelle f n'est pas paire, il suffit d'exhiber un seul réel x pour lequel f(x) diffère de f(-x) alors qu'il faudrait, pour prouver que la fonction est paire démontrer que l'égalité f(x) = f(-x) est vraie pour tout réel x appartenant à l'ensemble de définition de f.

Contre-exemple en pédagogie

En pédagogie, la donnée de contre-exemples permet de mettre en évidence la nécessité de la présence de chacune des hypothèses d'un théorème.

Contre-exemple et conjecture

Dans la recherche mathématique, il est fréquent que soient émises des conjectures, c'est-à-dire des propriétés que l'on pense être justes. La découverte d'un contre-exemple permet d'arrêter la recherche d'une démonstration ou d'affiner les hypothèses nécessaires à la réalisation de la conclusion.

C'est ainsi que Fermat  conjectura que tous les nombres (où n est un entier naturel quelconque ; ils sont appelés nombres de Fermat) sont premiers ,  car il avait constaté que les nombres , , , et l'étaient.

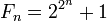
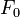
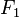
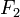
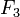
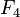
Euler prouva que cette conjecture était fausse en exhibant le contre-exemple suivant :  il calcula tout simplement , qui vaut 4294967297 et qui est divisible par 641.

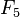
De même, la conjecture « Une fonction dérivable est-elle intégrale indéfinie de sa dérivée ? »" et la découverte de multiples contre-exemples comme celui de l'escalier de Cantor ont permis aux mathématiciens d'affiner les concepts d'intégrale et de primitive.

Trouver un contre-exemple pour prouver qu'une proposition est fausse est souvent tout aussi difficile que de trouver une démonstration pour prouver qu'une proposition est vraie. De même, vouloir faire une preuve par l'exemple est souvent tout aussi difficile qu'une démonstration directe (sauf cas immédiat de preuve par l'exemple de propriétés existentielle).