Théorie des catégories - Définition

Remarques

• Il arrive parfois que l'on oublie les objets d'une catégorie et que l'on ne s'intéresse plus qu'aux flèches, en substituant la flèche identité à l'objet.
• Il existe la catégorie des petites catégories, où la classe des objets est un ensemble, ainsi que la catégorie des foncteurs d'une petite catégorie à une autre : les morphismes sont les transformations naturelles. On voit ici le rôle joué par la théorie des classes NBG.

Somme et produit d'une famille d'objets en théorie des catégories

Étant donnée une famille , la somme de la famille est la donnée d'un objet de et pour tout d'une flèche  vérifiant la propriété universelle :

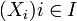
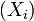
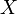
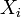
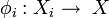
quels que soient l'objet et les flèches de il existe une unique flèche telle que le diagramme :

somme

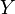
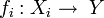
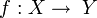
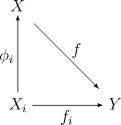
soit commutatif.

Étant donnée une famille , le produit de la famille est la donnée d'un objet de et pour tout d'une flèche  vérifiant la propriété universelle :

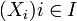
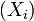
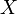
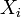
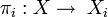
quels que soient l'objet et les flèches de il existe une unique flèche telle que le diagramme :

produit

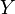
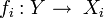
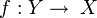
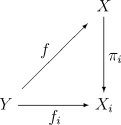
soit commutatif.

S'ils existent, les sommes et les produits sont uniques aux isomorphismes près.

On permute ces définitions en inversant les flèches des diagrammes : une somme [respectivement un produit] dans est un produit [respectivement une somme] dans sa duale.