Théorie des tresses - Définition
La liste des auteurs de cet article est disponible ici.
Mots de tresse
A isotopie près, une tresse abstraite peut toujours être représentée par une tresse géométrique qui ne contient jamais deux croisement à la même hauteur. Il est donc possible de projeter toute tresse dans le plan, afin d'obtenir un diagramme de tresse. Afin de ne pas perdre d'information vis-à-vis de l'espace en 3 dimensions il faut indiquer, lorsque deux brins se croisent, lequel passe devant l'autre.
Pour que les diagrammes de tresses et leur produit correspondent aux permutations et à leur composition il faut lire les diagrammes de tresses de bas en haut. Par exemple, le diagramme de tresses ci-contre a pour permutation
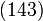
Ainsi prenons deux diagrammes de tresses
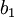
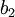
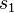
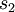
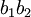
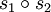
Pour étudier les tresses, il faut les comparer vis-à-vis de leur chemin et de leur permutation associée. Dans un diagramme de tresses, certains croisements sont indépendants les uns des autres.
Deux diagrammes de tresses sont dits 'isotopes' si on peut obtenir l'un à partir de l'autre en déplaçant les brins sans les « couper » et sans toucher aux extrémités.
La relation d'isotopie sur
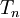
Deux diagrammes de tresses isotopes représentent la même permutation, mais la réciproque est fausse : deux diagrammes ayant la même permutation associée ne sont pas nécessairement isotopes.