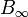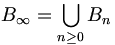Théorie des tresses - Définition

Introduction

En mathématiques, et plus précisément en topologie, la théorie des tresses est l'étude des tresses, objet mathématique formalisant ce qu'on appelle tresse (ou natte) dans la vie courante. Les tresses ont une structure de groupe naturelle, et possèdent des liens profonds avec des domaines divers des mathématiques et de la physique : topologie, théorie des noeuds, algèbre, combinatoire algébrique, physique statistique...

Définitions

Les groupes de tresses peuvent être définis de différentes manières équivalentes, illustrant les relations qu'ils entretiennent avec différents domaines des mathématiques.

Tresses géométriques

Exemple de tresse à trois brins

Soit un ensemble de n points de le disque unité ouvert de .

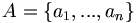
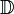
On appelle brin le graphe d'une application b continue de dans le disque unité ouvert de , dont les extrémités b(0) et b(1) appartiennent à A.

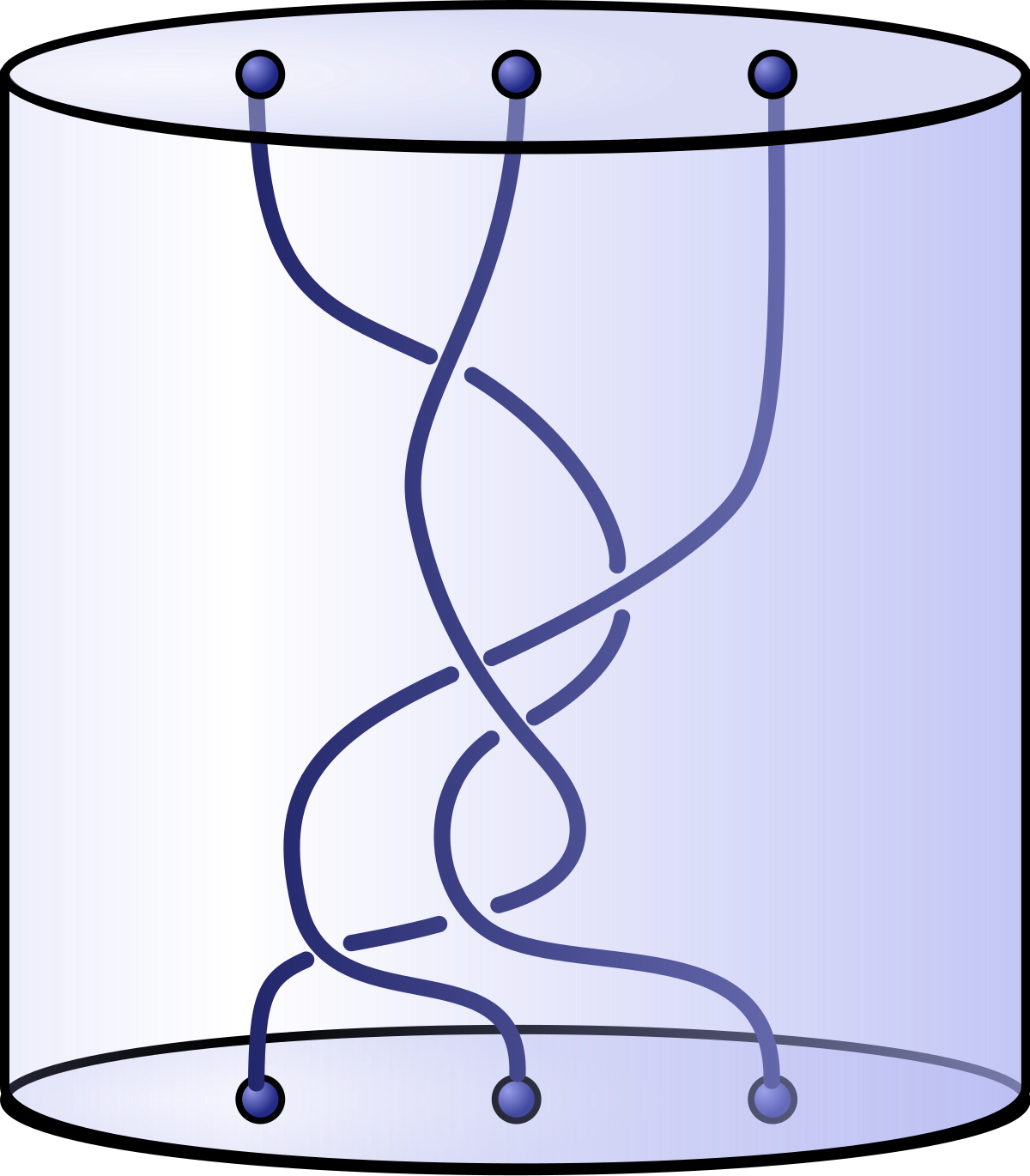
On appelle tresse géométrique à n brins la réunion de n brins disjoints. On considère que deux tresses géométriques représentent la même tresse "abstraite" si elle peuvent être obtenue l'une à partir de l'autre en bougeant les brins continument, sans que les brins ne se traversent ni ne se détachent à leurs extrémités. On dit alors que les deux tresses géométriques sont isotopes.

On définit une loi de composition sur l'ensemble des tresses géométriques, telle que le produit de deux tresses est obtenus simplement en les empilant l'une au-dessus de l'autre. Ce produit est associatif et compatible avec la relation d'isotopie. Le produit d'une tresse avec son image dans un miroir horizontal est isotope à la tresse triviale (sans croisement), dont la classe d'équivalence joue le rôle d'élément neutre. Ceci permet donc également de définir l'inverse d'une tresse. Finalement, l'ensemble des tresses géométriques à n brins quotienté par la relation d'isotopie est un groupe, noté B_n.

Générateurs et relations

Le groupe de tresses est le groupe engendré par les générateurs et les relations

1. si
2. sinon.

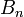
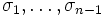
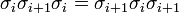
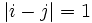
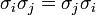
Groupe fondamental

On définit ce qu'on appelle un espace de configuration . Autrement dit, cet espace est l'ensemble des n-uplets de nombres complexes dont tous les éléments sont distincts. On peut interpreter physiquement cet espace en remarquant qu'un nombre complexe représente les coordonnées d'un point dans un plan, ainsi l'espace de configuration peut être vu comme l'ensemble des configurations dans lesquelles peuvent se trouver n particules dans un plan (la condition refletant simplement le fait que deux particules ne peuvent pas se trouver au meme endroit).

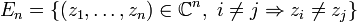
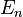
On remarque par ailleurs qu'en général, les brins d'une tresse n'arrivent pas dans le meme ordre qu'au départ. Par exemple, sur le premier dessin, le brin qui part d'en haut à gauche arrive en bas à droite. Il existe par contre des tresses dont tous les brins arrivent à la meme position que celle dont ils sont partis. Une telle tresse est appelée tresse pure. L'ensemble des tresses pures forme un sous groupe du groupe de tresses.

Le lien entre ces deux notions est le suivant : le groupe fondamental de est le groupe de tresses pures à n brins, noté .

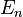
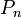
Groupes de tresses

En quotientant par la relation d'isotopie on obtient une structure de groupe sur l'ensemble des diagrammes de tresses à brins. On note et on appelle « groupe de tresses à n brins » le groupe ainsi obtenu. L'élément neutre étant bien évidemment la classe du diagramme trivial, l'inverse d'un diagramme est le diagramme obtenu en prenant son image miroir, comme on le voit sur l'exemple ci-dessous.

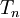
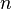
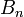
Par simplification on appelle tresse à brins un élément de .

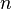
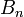
On plonge dans en transformant les tresses à brins en tresses à brins de la manière suivante. On ajoute à droite un ème brins qui n'en croise aucun autre, comme on le voit dans l'exemple suivant:

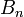
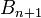
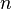
On note , et on appelle « groupe de tresses », le groupe .