Treillis (ensemble ordonné) - Définition
La liste des auteurs de cet article est disponible ici.
Cas particuliers
Un ensemble ordonné dans lequel chaque couple d'éléments possède une borne supérieure (ou une borne inférieure) est un demi-treillis.
Un treillis est dit distributif si la loi
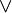


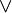
Un treillis est dit borné s'il possède un maximum et un minimum.
Un treillis borné est dit complémenté si chacun de ses éléments x possède un complément y vérifiant
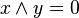
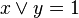
Un treillis distributif borné et complémenté s'appelle aussi une algèbre de Boole.
Un treillis E est dit complet si toute partie de E possède une borne supérieure, ou encore (ce qui dans un ensemble partiellement ordonné est équivalent) si toute partie de E possède une borne inférieure ; on dit aussi que E est un espace complètement réticulé. Un treillis complet est borné. (En informatique théorique, l'acronyme anglais CPO, bien sa traduction littérale soit « ordre partiel complet » , a un sens différent.)
Dans un treillis E possédant un minimum que l'on note 0, les atomes sont les éléments minimaux de E \ {0}. Par exemple dans le treillis de l'ensemble des parties d'un ensemble, les atomes sont les singletons.
Dualité
Si (E,
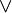


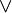
Théorème de dualité : Si un théorème T est vrai pour tous les treillis alors le théorème dual de T, obtenu en remplaçant toutes les occurrences de