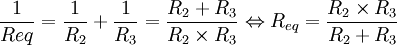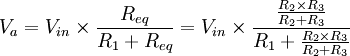Diviseur de tension - Définition
Le pont diviseur de tension est un montage électronique simple permettant d'obtenir une tension proportionnelle à une autre tension.
Constitution
Un pont diviseur de tension est constitué de deux résistances en série. La tension d'alimentation est appliquée à l'ensemble des résistances tandis que la tension de sortie est prise aux bornes d'une d'entre elles.
Pont diviseur de tension non chargé
Dans ce type de montage, les résistances R1 et R2 sont en série. Il n'y a pas de problème particulier et on obtient directement l'équation suivante :
Démonstration
- Req = R1 + R2 (association de R1 et R2 en série)
-
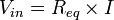
-
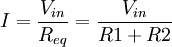
-
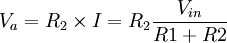
- soit :
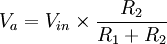
Pont diviseur de tension chargé
Les résistances R2 et R3 sont en parallèle. Le principe est de transformer les deux résistances R2 et R3 en une seule (Req) pour pouvoir calculer la tension de sortie par la suite dans l'équation en rapport avec le pont diviseur de tension.
Finalement, on a :