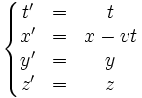Transformation de Galilée - Définition
Les transformations de Galilée désigne le groupe de transformations qui permet de lier deux systèmes de coordonnées de deux référentiels galiléens, c'est-à-dire en mouvement relatif uniforme en mécanique newtonienne.
Les équations de la transformation, apparemment évidentes, sont erronées lorsque la vitesse relative des référentiels s'approche de la vitesse de la lumière. Dans ces conditions, il faut les remplacer par le groupe des transformations de Lorentz.
Soient (x, y, z, t) les coordonnées d'un point dans un référentiel A, et (x', y', z', t') les coordonnées de ce point dans le référentiel A'. Si A' est en mouvement uniforme de vitesse v dans la direction x, relativement à A, alors on a :