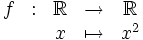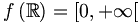Ensemble d'arrivée - Définition
Pour une fonction donnée f: A → B, l'ensemble B est appelé l'ensemble d'arrivée ou codomaine de f.
L'ensemble d'arrivée ne doit pas être confondu avec l'image de f, f(A), qui est en général seulement un sous-ensemble de B.
Exemple
Soit la fonction f sur l'ensemble des nombres réels définie par
L'ensemble d'arrivée de f est

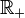
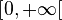
Nous aurions pu définir la fonction g ainsi
Tandis que f et g ont le même effet quand elles sont appliquées à un nombre réel donné, les fonctions sont différentes puisqu'elles ont des ensembles d'arrivée différents.
L'ensemble d'arrivée peut avoir un effet sur la surjectivité d'une fonction; dans notre exemple, g est une surjection alors que f ne l'est pas.
Voir aussi: Ensemble de définition