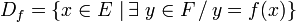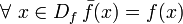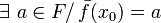Ensemble de définition - Définition
En mathématiques, l' ensemble de définition D f d'une fonction f dont l' ensemble de départ est noté E et l' ensemble d'arrivée F , est l'ensemble des antécédents de f, c'est-à-dire l'ensemble des éléments de E que f met en relation avec des éléments de F ; c'est donc l'ensemble des éléments x de E pour lesquels f ( x ) existe :
D f est encore appelé domaine de définition de f ou domaine de f.
Il ne faut pas confondre le domaine de définition d'une fonction f ( pour mémoire : D f ) avec son ensemble de départ ( pour mémoire : E ). Il arrive toutefois que les deux soient égaux : la fonction est alors une application. Elle est dite dans ce cas bien définie ou définie partout dans E.
A titre de contre-exemple, considérons la fonction 
.
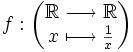
Cette fonction n'est pas définie en 0 : " f ( 0 ) " n'existe pas.
L'ensemble de définition de cette fonction est donc 
(rappel : 
). Il diffère de son ensemble de départ, 
; cette fonction n'est donc pas une application.
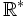
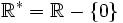
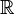
Cependant, il est toujours possible de transformer une fonction en application, par exemple en la restreignant à son domaine de définition. Cette restriction est notée habituellement " 
". C'est une application par construction.
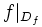
Ainsi, dans notre exemple, la fonction 
est bien une application.
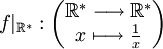
Une autre solution pour transformer une fonction en application consiste à la prolonger, c'est-à-dire choisir une image dans l'ensemble d'arrivée pour chacun des éléments sans image de l'ensemble de départ. En particulier, si une fonction numérique f n'est pas définie en un point x 0 , il est possible de la prolonger en ce point en la remplaçant par une autre fonction, appelée prolongement de f en x 0 et notée habituellement " 
", et telle que :
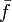
- le prolongement de f est égal à f sur D f :
- le prolongement de f a une valeur définie, a, au point x 0 :
Ainsi, dans notre exemple, on peut transformer la fonction 
en application en la prolongeant à l'origine par : 
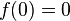
Remarque : assez souvent, pour alléger les notations, le prolongement est noté de la même manière que la fonction initiale. Cette ambiguïté est sans conséquence si le prolongement est explicité et remplace aussitôt et définitivement la fonction initiale.