Nombre réel - Définition

Introduction

En mathématiques, un nombre réel est un objet construit à partir des nombres rationnels, qui modélise la notion de longueur et d'autres grandeurs physiques.

L'ensemble des nombres réels, noté R, est l'union de l'ensemble des nombres rationnels (qui peuvent s'écrire sous forme de fraction) et de l'ensemble des nombres dont le développement décimal est infini non périodique, tels la racine carrée de 2 et π. Ces derniers sont appelés nombres irrationnels. Parmi les nombres réels on distingue également les nombres algébriques et les nombres transcendants.

Le terme de nombre réel apparaît chez Georg Cantor en 1883 dans ses publications sur les fondements de la théorie des ensembles. C'est un rétronyme, donné en réponse à la découverte des nombres imaginaires. Cependant, il est déjà présent dans un livre de Prestet et Malebranche en 1689 et peu après, en 1697, dans un livre de Thomas Fantet de Lagny. Selon le site Earliest Known Uses of some of the words in mathematics, l'adjectif réel fut utilisé pour la première fois en 1637 par René Descartes, en opposition à racines imaginaires. D'autres sens apparaissent également dans des traités de théologie/philosophie à la même époque.

Les nombres réels sont au centre de la discipline mathématique de l'analyse réelle, à laquelle ils doivent une grande part de leur histoire. La notation originale de l'ensemble des nombres réels est . Les lettres grasses étant difficiles à écrire sur un tableau ou une feuille, on utilise la notation , et en écriture manuscrite on ne double généralement que la barre verticale du R.

Représentation de la droite des réels avec des exemples de constantes réelles

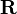
Dans la vie courante

Les nombres réels sont utilisés pour représenter n'importe quelle mesure physique telle que : le prix d'un produit, la durée entre deux événements, l'altitude (positive ou négative) d'un site géographique, la masse d'un atome ou la distance de la galaxie la plus proche. Ces mesures dépendent du choix d'une unité de mesure, et le résultat s'exprime comme le produit d'un nombre réel par une unité. Les nombres réels sont utilisés tous les jours, par exemple en économie, en informatique, en mathématique, en physique ou en ingénierie.

Le plus souvent, seuls certains sous-ensembles de réels sont utilisés :

• les entiers naturels,
• les entiers relatifs,
• les nombres décimaux, qui sont les réels que l'on peut écrire exactement en base 10 ;
• les nombres rationnels, exprimables sous forme de fractions à numérateurs et dénominateurs entiers,
• les nombres algébriques, qui comprennent notamment tous les nombres que l'on peut écrire en utilisant les quatre opérations élémentaires et les racines.
• les nombres calculables, qui comprennent la quasi-totalité des nombres utilisés en science et en ingénierie (notamment e et π).

Bien que tous ces sous-ensembles des réels soient de cardinal infini, ils sont tous dénombrables et ne représentent donc qu'une infime partie de l'ensemble des réels. Ils ont chacun des propriétés propres. Deux sont particulièrement étudiés par les mathématiciens : les nombres rationnels et les nombres algébriques ; on appelle « irrationnels » les réels qui ne sont pas rationnels et « transcendants » ceux qui ne sont pas algébriques.

En science

La physique utilise les nombres réels dans l'expression des mesures pour deux raisons essentielles :

• Les résultats d'un calcul de physique utilisent fréquemment des nombres qui ne sont pas rationnels, sans que les physiciens ne prennent en compte la nature de ces valeurs dans leurs raisonnements car elle n'a pas de sens physique.
• La science utilise des concepts comme la vitesse instantanée ou l'accélération. Ces concepts sont issus de théories mathématiques pour lesquelles l'ensemble des réels est une nécessité théorique. De plus, ces concepts disposent de propriétés fortes et indispensables si l'ensemble des mesures est l'espace des nombres réels.

En revanche, le physicien ne peut réaliser des mesures de précision infinie. La représentation numérique du résultat d'un calcul peut être approchée aussi précisément qu'il le souhaite par un nombre décimal. Dans l'état actuel de la physique, il est même théoriquement impossible de réaliser des mesures de précision infinie. C'est pourquoi, aussi bien pour des besoins expérimentaux que théoriques, si le physicien calcule les mesures dans , il exprime les résultats numériques sous forme de nombres décimaux.

Ainsi le physicien utilise les propriétés des nombres réels qui permettent de donner un sens aux mesures qu'il réalise et offrent des théorèmes puissants pour démontrer ses théories. Pour les valeurs numériques, il se contente des nombres décimaux. Quand il mesure la distance que parcourt un point matériel sur un cercle complet, il utilise la valeur π sans se poser de question sur son existence, mais un nombre de décimales souvent petit lui suffit pour les calculs.

Enfin, bien que les nombres réels puissent représenter n'importe quelle grandeur physique, les nombres réels ne sont pas les mieux adaptés pour l'étude de très nombreux problèmes physiques. Des « sur-ensembles » construits autour des réels ont été créés pour pouvoir manipuler certains espaces physiques. Par exemple :

• l'espace , pour modéliser des espaces, par exemple de dimension 2, 3 (ou plus) ;
• l'ensemble des nombres complexes dont la structure possède des propriétés plus fortes que celle de l'ensemble des nombres réels.

Autres remarques sur la notion de « développement décimal infini »

Tout nombre réel peut être représenté sous la forme de « nombre à développement décimal infini ». Cette définition peut sembler plus simple que d'autres utilisées couramment par les mathématiciens, comme par exemple la limite d'une suite convergente. Pourtant, elle apparaît rapidement comme peu adaptée et implique des définitions et des démonstrations bien plus complexes. En effet les nombres réels sont intéressants pour la structure et les propriétés de l'ensemble qu'ils forment : addition, multiplication, relation d'ordre, et les propriétés qui lient ces notions. Ces propriétés sont mal reflétées par la définition « développement décimal infini » et des problèmes théoriques apparaissent :

• Certains nombres possèdent deux représentations.

Par exemple, le nombre x=0,9999... (les 9 se poursuivent à l'infini), vérifie l'équation 10x = 9+x. Le nombre y=1,000000... (les 0 se poursuivent à l'infini) en est également solution. Or l'existence et l'unicité de solution à l'équation 10t = 9+t, d'inconnue t, sont deux propriétés essentielles pour une définition univoque des réels. Pour remédier à cette situation, il devient nécessaire d'identifier les représentations décimales qui sont solutions d'une même équation : la définition devient plus complexe.

• Utiliser un développement décimal fait jouer un rôle particulier à la base 10.

Cette difficulté n'est pas insurmontable. Elle est résolue par l'utilisation d'une base quelconque : on parle alors de développements en base p. Il est alors possible de démontrer que les ensembles construits à partir de ces bases sont isomorphes et que les propriétés des nombres réels sont valables dans toutes ces bases. Cependant les démonstrations deviennent lourdes, et la définition perd de sa simplicité.

• Enfin les algorithmes naturels pour effectuer une addition ou une multiplication, trouvent leur limite du fait de la double représentation des nombres décimaux.

En effet, les « retenues » se calculent de la droite vers la gauche, et un algorithme effectif demande de ne traiter qu'un nombre fini de décimales (puisqu'il ne peut effecteur qu'un nombre fini d'opérations), c'est-à-dire de tronquer les nombres sur lesquels on calcule : il se peut donc qu'en tronquant aussi loin que l'on veut, on n'ait jamais la moindre décimale exacte, par exemple sur le calcul 0,33...+0,66...=1. Surmonter cette difficulté demande de faire appel à des notions de convergence, qui amènent naturellement vers d'autres modes de définition des réels.

Cependant, une fois établie la structure de l'ensemble des nombres réels, la notation par développement décimal permet des calculs effectifs, en gardant à l'esprit que ce n'est pas tant les décimales exactes d'un nombre qui comptent, que la position du nombre vis-à-vis des autres réels.