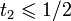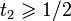Algorithme de De Casteljau - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Historique - L'algorithme dans le cas de courbes de Bézier - L'algorithme de calcul d'un point - L'algorithme dans le cas de surfaces de Bézier

L'algorithme de calcul d'un point

Principe

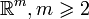
Considérons une courbe de Bézier définie par les points de contrôles $P_0,\dots,P_N$ , où les $P i$ sont des points de $\R^m, m \geqslant 2$ . Ici on souhaite simplement calculer le point de paramètre $t \in [0,1]$ .

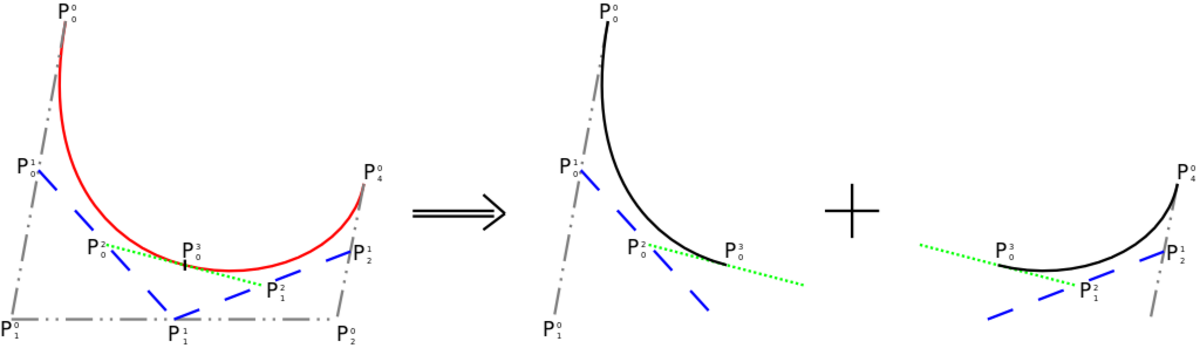
Principe de l'algorithme de De Casteljau

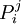
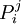
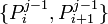
Comme on peut le voir sur l'image, en calculant les barycentres de paramètres ${t,1 - t}$ des points de contrôle consécutifs de la courbe, puis les barycentres de même paramètres de ces barycentres et ainsi de suite itérativement, on définit de cette manière une suite de listes de points que l'on va indexer $P^j_i$ , où $P^j_i$ est le barycentre de $\{P^{j-1}_i,P^{j-1}_{i+1}\}$ . La dernière liste ne contient en fait qu'un point, qui est le point de la courbe de paramètre $t$ .

Algorithme

En pseudo-code, ceci donne:

       // Calcul des points intermédiaires       Pour j de 1 à N faire       |       | Pour i de 0 à N-j faire       | |       | | T[i][j] = t*T[i+1][j-1] + (1-t)*T[i][j-1]       | |       |       Afficher T[0][N] // Afficher (ou stocker) le point

Eléments de preuve de l'algorithme

Pour démontrer l'algorithme, il faut prouver par récurrence limitée que

$\forall i \in [0,n], \forall t \in [0,1], B(t) = \sum_{k=0}^{n} P^{0}_{k} B^{n}_{k}(t) = \sum_{k=0}^{n-i} P^{i}_{k} B^{n-i}_{k}(t)$

Et d'appliquer la formule en $i = n$ , ce qui nous donne le résultat directement.

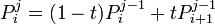
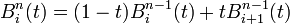
La récurrence se démontre facilement en utilisant la propriété de construction des points $P_i^j = (1-t)P_i^{j-1} + tP_{i+1}^{j-1}$ pour séparer la somme en deux, puis en faisant un changement d'indice et en utilisant une propriété des polynômes de Bernstein $B_i^n(t) = (1-t)B_i^{n-1}(t) + t B_{i+1}^{n-1}(t)$ pour regrouper les deux sommes. 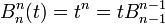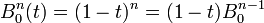Pour réintégrer les cas particuliers, il faut utiliser deux autres propriétés des polynômes de Bernstein: $B^n_n (t) = t^n = t B^{n-1}_{n-1}$ et $B^n_0 (t) = (1-t)^n = (1-t) B^{n-1}_{0}$

Complexité

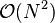
L'exécution d'une étape de l'algorithme est quadratique en nombre de points de contrôle de la courbe (la boucle imbriquée donne lieu à $\mathcal{O}(N^2)$ opérations).

L'algorithme dans le cas de surfaces de Bézier

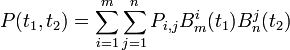
Une surface de Bézier est définie par une double somme de points: $P(t_1,t_2) = \sum_{i=1}^m \sum_{j=1}^n P_{i,j} B_m^i (t_1) B_n^j (t_2)$

Le principe de l'algorithme est de réécrire la formule sous la forme:

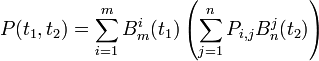
$P(t_1,t_2) = \sum_{i=1}^m B_m^i (t_1) \left( \sum_{j=1}^n P_{i,j} B_n^j (t_2) \right)$

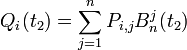
et en renommant $Q_{i} (t_2) = \sum_{j=1}^n P_{i,j} B_n^j (t_2)$ , on obtient

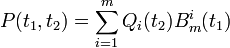
$P(t_1,t_2) = \sum_{i=1}^m Q_{i} (t_2) B_m^i (t_1)$

En remarquant que les $Q i (t 2)$ sont des points de courbes de Bézier, le principe de l'algortithme arrive. A chaque itération de l'algorithme

calculer les points $Q i (1 / 2)$ et les restrictions des courbes de Bézier pour chaque $i$ par l'algorithme de De Casteljau sur les courbes
calculer puis afficher/stocker les points de la courbe de Bézier de points de contrôle les $Q i (1 / 2)$ par l'algorithme de De Casteljau sur les courbes
appliquer récursivement l'algorithme sur les deux surfaces obtenues en regroupant les restrictions pour $t_2 \leqslant 1/2$ et $t_2 \geqslant 1/2$

L'algorithme dans le cas de courbes de Bézier

- Introduction - Historique - L'algorithme dans le cas de courbes de Bézier - L'algorithme de calcul d'un point - L'algorithme dans le cas de surfaces de Bézier

🎶 Un dinosaure qui chantait comme un oiseau découvert en Chine

☄️ Pluie d'étoiles filantes des Perséides: le rendez-vous à ne pas manquer

🌐 L'espace De Sitter: une explication si simple pour l'origine de notre Univers

⚠️ Un édulcorant utilisé dans les aliments light pourrait causer des AVC

🕷️ Découverte: les araignées n'ont pas une origine terrestre

📜 Des remèdes médicaux du Moyen Âge révélés, et certains fonctionnent !

⚫ Ces électrons froids remettent en question nos connaissances des trous noirs

🩺 Peut-on vraiment boire des microplastiques ?

🐋 Voici comment les déjections des baleines nous permettent de respirer

⏳ Ces édulcorants accéléreraient la puberté

👀 Découverte d'une multitude de trous noirs cachés dans l'Univers primordial

🌡️ Quelle est la température maximale que la Terre peut atteindre ?

💡 Cette nouvelle expérience montre qu'Einstein avait tort sur la lumière

🌵 Comment les plantes résistent-elles à la chaleur ?

👽 Sans le vouloir, nous communiquons notre position à d'éventuelles civilisations extraterrestres

📏 Les ancêtres humains avaient des 'hommes' bien plus grands que les 'femmes'

🧲 Une question résolue sur l'origine du champ magnétique terrestre

🍳 Ceci n'est pas un œuf, et il ne faut surtout pas le manger

🥔 La tomate: l'origine surprenante de nos pommes de terre

⛈️ Qu'est-ce que la foudre ?

🔵 Quel est le secret du bleu maya ?

🚨 L'obésité, un facteur de l'explosion des décès par cancer

🔭 Notre place dans l'Univers serait particulière, et cela explique bien des choses

🍉 Pourquoi les fruits d'été sont-ils si sucrés ?

🔭 Des forces cachées aux confins du Système solaire ?

🌍 Découverte de structures anciennes cachées sous l'Antarctique, et cela nous concerne directement

📢 Comment les cigales font-elles leur bruit ?

🌊 C'est énorme: 27 millions de tonnes de plastiques déversés dans l'Atlantique Nord

🔭 Cette observation suggère que tout pourrait venir de la ceinture d'astéroïdes

🦴 Comment les pythons digèrent-ils les os sans laisser de trace ?

💫 Comment un pulsar milliseconde a trompé les astronomes pendant des années ?

🌱 Par évolution dirigée, le MIT a fortement amélioré l'efficacité de la photosynthèse

🌍 Une météorite a-t-elle modifié le Grand Canyon il y a 56 000 ans ?

🕒 Le lien surprenant entre repas tardifs, santé et prise de poids

💥 Cette collision de trous noirs est si massive qu'elle fait trembler nos lois de l'astrophysique

🩺 Cancer: des cellules "oubliées" passent à l'offensive

🔭 Quel est cet objet mystérieux, lié à Neptune dans une orbite jamais vue auparavant ?

🍄 Découverte surprenante: vivre 25 ans de plus grâce aux "champignons magiques" ?

🩺 L'âge des premières règles est un indicateur de la santé à venir

⚛️ Cette découverte pourrait expliquer pourquoi notre Univers existe

🌋 Découverte majeure sous Yellowstone grâce à l'IA

🏹 Violence préhistorique: découverte d'un surprenant homicide raté

🌌 Des scientifiques découvrent dans l'Univers un gigantesque filament de matière "manquante"

🐱 Ce chat a aidé à découvrir un virus inconnu... deux fois !

🪐 Cette planète provoque la fureur de son étoile

👂 Et si nous pouvions entendre une caresse ?

👑 Cette découverte archéologique révèle les prémices des pharaons

🦈 Le requin bleu peut changer de couleur, comme un caméléon

🌞 La NASA dévoile les images les plus proches jamais prises du soleil

⏳ Il est maintenant possible de mesurer le vieillissement avec précision

Page générée en 0.257 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise