Courbe de Bézier - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les courbes de Bézier sont des courbes polynomiales paramétriques décrites pour la première fois en 1962 par l'ingénieur français Pierre Bézier qui les utilisa pour concevoir des pièces d'automobiles à l'aide d'ordinateurs. Elles ont de nombreuses applications dans la synthèse d'images et le rendu de fontes. Elles ont donné naissance à de nombreux autres objets mathématiques.
Il existait avant Bézier des courbes d'ajustement nommées splines, mais dont le défaut était de changer d'aspect lors d'une rotation de repère, ce qui les rendait inutilisables en CAO. Bézier partit d'une approche géométrique fondée sur la linéarité de l'espace euclidien et la théorie, déjà existante, du barycentre : si la définition est purement géométrique, aucun repère n'intervient puisque la construction en est indépendante, ce qui n'était pas le cas pour les splines (les splines conformes aux principes de Bézier seront par la suite nommée B-splines).
Théorie générale
Pour n+1 points de contrôle (
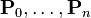
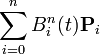
![t \in[0,1]](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d9a06fde4663cdd5b1ba693e9127232f_ce76be6544934df881b7082a83aabd2d.png)
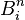
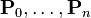
Remarque : Puisque
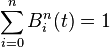
Propriétés :
- La courbe est à l'intérieur de l'enveloppe convexe des points de contrôle.
- La courbe commence par le point
-
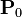
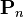
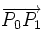
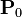
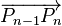
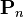
- Une courbe de Bézier est infiniment dérivable (de classe
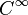
- La courbe de Bézier est un segment si et seulement si les points de contrôle sont alignés.
- Chaque restriction d'une courbe de Bézier est aussi une courbe de Bézier.
- Un arc de cercle ne peut pas être décrit par une courbe de Bézier, quel que soit son degré.
- Le contrôle de la courbe est global : modifier un point de contrôle modifie toute la courbe, et non pas un voisinage du point de contrôle.
- Pour effectuer une transformation affine de la courbe, il suffit d'effectuer la transformation sur tous les points de contrôle.
Exemples
- Courbe de Bézier linéaire (de degré 1)
Les points de contrôle P0 et P1 définissent la courbe de Bézier donnée par l'équation :
![\mathbf{B}(t)=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \mbox{ , } t \in [0,1].](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/3e9b0196234c9ee410c67dfea9235c4b_90d485d7a08ec0030ba8c3a04699647b.png)
Il s'agit donc du segment [P0, P1].
- Courbe de Bézier quadratique (de degré 2)
Une courbe de Bézier quadratique est la courbe B(t) définie par les points de contrôle P0, P1 et P2.
![\mathbf{B}(t) = (1 - t)^{2}\mathbf{P_0} + 2t(1 - t)\mathbf{P_1} + t^{2}\mathbf{P_2} \mbox{ , } t \in [0,1].](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a5a52a4198f82a125b74f69c1899da32_ab234f7da8a9b6240caa200d7de925bf.png)
- Courbe de Bézier cubique (de degré 3)
Ce sont les courbes de Bézier les plus utilisées (car elles permettent d'assurer la continuité en tangence et en courbure de deux courbes raccordées). Une courbe de Bézier cubique est la courbe B(t) définie par les points de contrôle P0, P1, P2 et P3. Sa forme paramétrique est :
![\mathbf{B}(t)=\mathbf{P_0}(1-t)^3+3\mathbf{P_1}t(1-t)^2+3\mathbf{P_2}t^2(1-t)+\mathbf{P_3}t^3 \mbox{ , } t \in [0,1].](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0b16fa087f21a2910fb2eae9f1cea710_4a8cbf6c8cc32eeafae4d4040beaed5b.png)
- Courbe de Bézier de degré supérieur à 3
Elles sont rarement utilisées. On préfère se ramener à l'utilisation de courbes cubiques que l'on raccorde. Pour cela, il faut et il suffit que le dernier point d'une courbe soit le premier d'une autre. On obtient ainsi une courbe continue.
Par exemple, pour une courbe définie par les points A, B, C, D, E, F et G, on utilise les courbes cubiques définies par A, B, C, et D, et par D, E, F, et G et la continuité est ainsi assurée. Pour avoir une courbe C1 en D, il faut que [C, D] = [D, E], et si en plus on veut qu'elle soit C2 en D, alors [B, D] = [D, F], et de même pour les dérivées successives.
