Algorithme de De Casteljau - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'algorithme de De Casteljau est un algorithme récursif trouvé par Paul de Casteljau pour approximer efficacement les polynômes écrit dans la base de Bernstein.
Cet algorithme peut être utilisé pour dessiner des courbes et des surfaces de Bézier. L'idée principale dans ce cas repose sur le fait qu'une restriction d'une courbe de Bézier est aussi une courbe de Bézier. L'algorithme calcule de manière efficace le point de parametre t = T et les points de contrôle des courbes de la restriction à
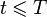
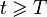
Cet algorithme semble ne plus être le plus efficace car il ne permettrait pas d'utiliser l'antialiasing étant donné qu'il travaille pixel par pixel et ne donne pas d'information sur la tangente.
Historique
Historiquement, c'est avec cet algorithme que les travaux de M. De Casteljau commençaient en 1959 chez Citroën. Ils étaient publiés comme des rapports techniques, tenus très au secret par Citroën.
Ces travaux restèrent inconnus jusqu'en 1975 quand W. Böhm en a pris connaissance et les a rendu public. Cet algorithme a été très utile pour l'informatique qui utilise les courbes de bézier dans de nombreux cas (logiciels de dessin, de modélisation, ...), et sans lequel le développement de l'utilisation des courbes de Pierre Bezier n'aurait pas pu se faire.
L'algorithme dans le cas de courbes de Bézier
Considérons encore une courbe de Bézier définie par les points de contrôles

 .
.
Principe
On va ici appliquer l'algorithme précédent pour trouver le point de paramètre 1 / 2, et conserver les barycentres intermédiaires. En effet, la courbe de Bézier de points de contrôle
![P^i_0,i\in [0,N]](https://static.techno-science.net/illustration/Definitions/autres/7/71e9a7910bf6b818cd2a89bb60ecf857_268c76190a45f48a14fd3e69a218842c.png)
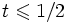
![P^{N-i}_i,i\in [0,N]](https://static.techno-science.net/illustration/Definitions/autres/2/296ea268fc616ec238e4e88fe90ccad4_9d2f5626e85f8ba01368fe72d0330398.png)
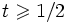
On affiche ou mémorise le point de paramètre 1 / 2 (qui est
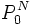
Plutôt que le paramètre 1 / 2, on pourrait prendre un paramètre quelconque et l'algorithme fonctionnerait encore, mais le paramètre 1 / 2 est celui qui converge en moyenne le plus rapidement. Le paramètre 1 / 2 est aussi celui pour lequel les calculs sont les plus rapides quand l'on travaille en coordonnées entières : le calcul de chaque barycentre se fait par une addition et un décalage à droite pour chaque coordonnée, c'est à dire sans multiplication ni division.
Algorithme
- Initialisation: affecter le tableau des points de contrôle dans les
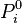
- Voir que le critère d'arrêt n'est pas vérifié: il y a plusieurs possibilités dont:
- Si on fait tous les calculs avec des nombres entiers, un choix peut être de s'arrêter lorsque tous les points sont confondus. (c'est-à-dire que la courbe n'est représentée que par un seul pixel)
- Si le calcul n'est pas fait sur des nombres entiers on peut s'arrêter quand les points sont distants d'une distance inférieure à une valeur choisie
- On effectue M itérations puis on relie les points obtenus (c'est-à-dire que l'on trace le polygone de Bézier), M étant déterminé empiriquement
- Calcul les points intermédiaires de l'algorithme : il y a deux méthodes possibles qui donnent finalement les mêmes points
- Méthode constructive (en construisant une suite de milieux): On définit itérativement les points
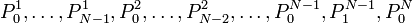
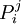
![[P^{j-1}_iP^{j-1}_{i+1}]](https://static.techno-science.net/illustration/Definitions/autres/8/87d3a2c3a80de24f97169ae50e4ef8a6_688a00241bbd11ba05b6951e2739fb10.png)
- Méthode matricielle (en construisant directement les points comme barycentre, les coefficients étant donnés par les matrices de De Casteljau) :
- Méthode constructive (en construisant une suite de milieux): On définit itérativement les points
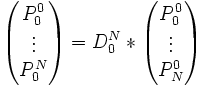
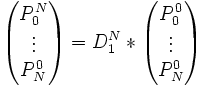
- Mémorisation: on mémorise le point
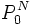
- Appel récursif: on appelle l'algorithme sur les deux courbes de Bézier intermédiaires définies par les points
![P^i_0,i\in [0,n]](https://static.techno-science.net/illustration/Definitions/autres/a/a9a712fb841e6e7b59bafcf07c37d4a3_3938041f00b24e4e2a8f9a2cbae96fff.png)
![P^{n-i}_i,i\in [0,n]](https://static.techno-science.net/illustration/Definitions/autres/9/94083b141e75e344321b3af5902b4396_ad2ab06f3b9716a2a4e0c6bcd75d053b.png)
Voici un exemple d'implémentation de l'algorithme en pseudo-code avec pour critère d'arrêt l'égalité des points (on travaille donc sur des entiers) et la construction constructives pour calculer les points intermédiaires:
Entrée: tableau T[0][0...N] des coordonnées des points de contrôle.
Si T[0][0] = T[0][1] = ... = T[0][N] //si le critère d'arrêt est vérifié on s'arrête alors | | fin | Sinon //pour dessiner | | // Calcul des points intermédiaires | Pour i de 1 à N faire | | | | Pour j de 0 à N-i faire | | | | | | T[i][j] = milieu de T[i-1][j] T[i-1][j+1] | | Afficher T[N][0] // Afficher (ou stocker) le point milieu | | // Construction des courbes restreintes | Pour i de 0 à N faire | | | | T'[i] = T[i][0] | | T"[i] = T[N-i][i] | | // Appel récursif | de_Casteljau(T') | de_Casteljau(T")
Complexité
Si on prend comme critère d'arrêt un nombre d'appels récursifs constant, comme le nombre de points de contrôle est constant pendant les appels récursifs reste constant et qu'à chaque étape de récursion on double le nombre de courbes étudiées, la complexité de l'algorithme est en