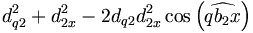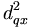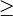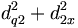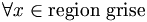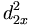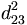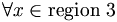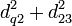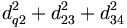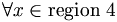Arbre d'axes principaux - Définition

Introduction

L’arbre d'axes principaux (en anglais : Principal Axis Tree), souvent abrégé PAT est un algorithme permettant de diviser un espace de points de manière efficiente en vue de résoudre rapidement le problème des plus proches voisins. Elle fut développée par James McNames en 2001.

L'algorithme obtenu permet d'effectuer des recherches de voisinage d'un point donnée en un temps moyen . Cet algorithme de recherche se base sur un élagage très rapide de l'arbre, grâce à la puissance de son critère d'élimination, tout en limitant l'espace de stockage nécessaire en mémoire informatique. Enfin, à l'intérieur d'une feuille donnée, l'algorithme utilise la recherche de distance partielle pour encore accélérer les calculs.

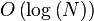
L'algorithme présente les caractéristiques suivantes, N étant le nombre de points présents dans l'espace :

• Temps de calcul préparatoire (prétraitement) en  ;
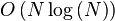
• Espace de stockage en  ;
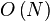
• Temps de recherche moyen en .

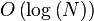
Construction de l'arbre

Schématiquement, la construction de l'arbre d'axe principal se déroule en 6 étapes :

• Soient N points à classer dans un nœud, considéré comme nœud racine, et n_c le nombre maximum de fils que peut avoir un nœud ;
• Attribuer les N points au nœud racine. Le nœud racine deviens le nœud en cours ;
  • Si le nombre de points assigné au nœud en cours est inférieur à n_c, le nœud est terminal et son traitement est terminé ;
  • Sinon, construire l'axe principal pour les points en cours et projeter orthogonalement ces points sur cet axe ;
• Partitioner l'ensemble des points projetés sur l'axe en n_c régions distinctes et manière à ce que chaque région contienne le même nombre de points, à une unité prêt ;
• Attribuer chaque région ainsi créée à un des n_c nœuds fils distinct et recommencer en 3 pour chacun de ces nœuds.

On obtient ainsi un arbre pour lequel l'ensemble des points est attribué à la racine. Ces points sont ensuite séparés en différentes régions, chacune correspondant à un fils de la racine. On peut, via l'axe principal qui a été sauvé à chaque étape, déterminer dans quelle région doit se situer un point de coordonnées données et donc savoir à quel nœud fils il est associé.

À partir de là, on peut déterminer dans quelle sous-région il se trouve et ainsi de suite jusqu'à atteindre une région terminale. Cette région terminale est caractérisée par la présence de peu de points (moins de n_c qui est généralement de l'ordre de 2 à une dizaine).

À noter que cet arbre présente au premier abord 2 avantages :

• Aucune région de l'arbre n'est vide, même partiellement ;
• L'axe principal sert à tout moment et est une droite, les problèmes sont donc linéaires.

Critère d'élimination

Critère d'élimination de l'algorithme, basé sur des projections orthogonales.

L'efficacité du critère d'élimination régit celle de tout algorithme de recherche. L'algorithme utilisé dans l'arbre des axes principaux tire la sienne de deux points :

• Un minimum de la distance entre un point situé dans une région et l'ensemble des points situé dans une autre région de l'espace se fait en utilisant uniquement des additions et des multiplications, sans connaître les coordonnées des points situés dans la deuxième région ;
• Par construction de l'arbre, pour chaque séparation entre deux régions à l'intérieur d'un nœud, un point doit se situer à la frontière, impliquant une réduction considérable des risque de sous-évaluation dus à la présence d'espaces vides.

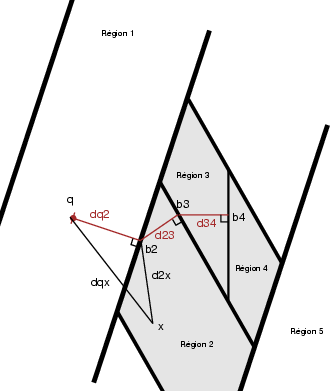
Pour comprendre le fonctionnement du critère d'élimination, le lecteur est invité à se référer à la figure ci-contre. Chaque nœud de l'arbre correspond à une région de l'espace. À partir d'informations fournies lors de la construction de l'arbre, le critère d'élimination est capable d'évaluer une distance minimum au-delà de laquelle se trouve n'importe quel point de la région. Si cette distance minimale est trop grande par rapport au proches voisins déjà trouvé, la région entière peut être éliminée. Les nœuds voisins sont encore plus loin, par construction de l'arbre, et sont eux aussi éliminés.

Dans la figure, la distance entre le point q, point situé dans la région 1 dont on cherche le voisinage, et x un point quelconque situé dans la région 2 est supérieure à la distance entre le point q et l'hyperplan séparant la région 1 de la région 2. Cet hyperplan étant, par construction, perpendiculaire à l'axe principal, la distance peut être calculée rapidement le long de cet axe, soit en dimension 1. La distance d_q2 est donc le minimum entre le point q et tout point de la région grisée. Si ce minima est supérieur à l'ensemble des point voisin de q déjà trouvée, la région grisée ainsi que la région 5 et au-delà peuvent être éliminés sans avoir à regarder les points présents dans ces régions.

Si le test échoue, il faut regarder de plus près ce qui se passe dans la région grisée (c'est-à-dire descendre dans le nœud correspondant). Soit le triangle formé par (qb₂x). Nous savons que l'angle est compris entre 90° et 180°. Son cosinus est donc négatif et un minima de peut être calculé par le théorème d'Al-Kashi :

	=

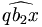
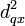
Le même raisonnement appliqué à une autre sous région donne :

Les points frontières b et les minimums des distances sont ainsi calculés récursivement par l'algorithme de recherche. Ces calculs de distances de points frontière se font extrêmement rapidement car ils peuvent être faits directement à partir de projections sur l'axe principal, et donc en dimension 1.