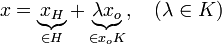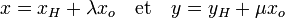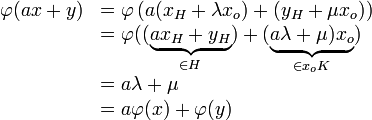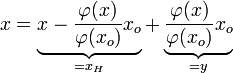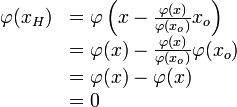Hyperplan - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Lien avec les formes linéaires - Caractérisation - Représentation des sous-espaces - Exemples

Introduction

En mathématiques, et plus particulièrement en algèbre linéaire, les hyperplans sont des sous-espaces vectoriels particuliers.

Définition

Soit E un $\mathbb K$ -espace vectoriel et H un sous-espace vectoriel de E.

On dit que H est un hyperplan de E si H est de codimension 1.

Remarques :

Dans un espace de dimension finie n, les hyperplans sont donc les sous-espaces vectoriels de dimension n-1.
Dans $\mathbb{R}^3$ , la notion d'hyperplan est confondue avec celle de plan, mais ce n'est plus vrai quand la dimension de l'espace est supérieure à 3.

Lien avec les formes linéaires

On montre que les hyperplans sont exactement les noyaux des formes linéaires non nulles.

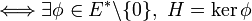
C'est-à-dire : H est un hyperplan de E $\Longleftrightarrow \exists \phi \in E^*\backslash\{0\}, \ H=\ker \phi$

Soit H un hyperplan de E. On cherche à construire une forme linéaire non nulle dont H est le noyau.

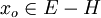
H est un hyperplan donc par définition il admet un supplémentaire dans E de dimension égale à 1. C'est donc une droite vectorielle engendrée par un $x_o \in E-H$ (x_o ne peut être nul car il n'appartient pas à H qui contient 0). On a donc

Tout vecteur x de E se décompose donc de la façon suivante:

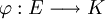
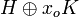
Posons une application $\varphi: E \longrightarrow K$ qui a tout vecteur de E associe le scalaire associé à x_o dans sa décomposition suivant $H \oplus x_o K$ . Montrons alors que $\varphi$ est linéaire: On prend deux vecteurs x et y quelconque de E qui se décomposent comme ci-dessus:

En prenant un scalaire $a \in K$ quelconque on obtient:

\begin{array}{ll} \varphi(ax+y)&=\varphi \left(a(x_H+\lambda x_o)+(y_H+\mu x_o)\right)\\ &=\varphi ((\underbrace{ax_H+y_H}_{\in H})+(\underbrace{a\lambda + \mu )x_o}_{\in x_o K})\\ &=a\lambda + \mu\\ &=a\varphi(x)+\varphi(y) \end{array}

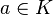
Ce qui montre que $\varphi$ est linéaire, de plus son ensemble d'arrivée est K, c'est donc bien une forme linéaire. De plus elle n'est pas nulle (par exemple x_o a pour image 1).

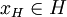
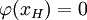
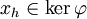
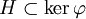
Prenons un $x_H \in H$ . Par décomposition $x H = x H + 0 x o$ donc $\varphi(x_H)=0$ et donc $x_h \in \ker \varphi$ . On a donc $H \subset \ker \varphi$ .

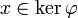
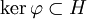
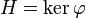
Réciproquement, soit $x \in \ker \varphi$ . Alors ce vecteur n'est pas engendré par x_o et donc appartient à H. On a donc $\ker \varphi \subset H$ et donc par double inclusion $H=\ker \varphi$ .

H est donc le noyau d'une forme linéaire non nulle.

Réciproquement, soit $\varphi$ une forme linéaire non nulle et H son noyau. Montrons que H est un hyperplan de E. Pour cela, on va montrer que H admet un supplémentaire de dimension 1.

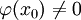
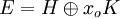
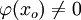
$\varphi$ est non-nulle, il existe donc un vecteur x_o de E non-nul tel que $\varphi(x_0) \neq 0$ . Montrons alors que $E=H\oplus x_o K$ . Soit x dans E. Comme $\varphi (x_o) \neq 0$ , on peut écrire la tautologie suivante:

x=\underbrace{x-\frac{\varphi(x)}{\varphi(x_o)}x_o}_{=x_H} + \underbrace{ \frac{ \varphi(x)}{ \varphi(x_o)}x_o}_{=y}

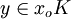
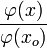
Il est clair que $y \in x_o K$ car $\frac{ \varphi(x)}{ \varphi(x_o)}$ est bien dans K.

D'autre part:

\begin{array}{ll} \varphi(x_H)&=\varphi\left(x-\frac{\varphi(x)}{\varphi(x_o)}x_o\right)\\ &=\varphi(x)-\frac{\varphi(x)}{\varphi(x_o)}\varphi(x_o)\\ &=\varphi(x)-\varphi(x)\\ &=0 \end{array}

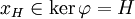
Donc $x_H \in \ker\varphi=H$ . Autrement dit, tout vecteur de E se décompose en somme d'un élément de la droite vectorielle engendrée par x_o et d'un élément du noyau H, ie $E = H + x o K$ . Montrons maintenant que cette somme est directe.

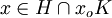
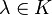
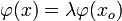
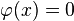
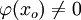
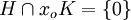
Soit $x \in H \cap x_o K$ . On peut donc écrire $x = λ x o$ avec $\lambda \in K$ . Et donc $\varphi (x) =\lambda \varphi(x_o)$ . Mais comme x est dans H on a également $\varphi(x)=0$ . C'est-à-dire $λ = 0$ (car $\varphi(x_o) \neq 0$ ) et donc x=0. D'où $H \cap x_o K = \{0\}$ et la somme est directe.

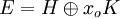
Par conséquent, $E=H\oplus x_o K$ soit, par définition:

H est un hyperplan de E.

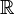
Interprétation de ce résultat dans le $\mathbb{R}\,\!$ -espace vectoriel $\mathbb{R}^3$ :

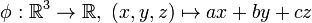
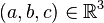
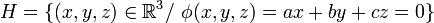
Toutes les formes linéaires sur $\mathbb{R}^3$ peuvent s'écrire sous la forme suivante : $\phi : \mathbb{R}^3 \rightarrow \mathbb{R},\ (x,y,z) \mapsto ax+by+cz$ avec $(a,b,c) \in \mathbb{R}^3$ fixé. Le résultat précédent nous indique que tout hyperplan de $\mathbb{R}^3$ peut s'écrire comme le noyau d'une forme linéaire. Autrement dit $H=\{(x,y,z) \in \mathbb{R}^3 / \ \phi(x,y,z) = ax+by+cz=0\}$

Ce lien entre hyperplan et noyau d'une forme linéaire exprime en fait la notion d'équation d'un hyperplan, donc ici d'un plan (vectoriel).

Caractérisation

On montre l'équivalence des propriétés suivantes :

$H$ est un hyperplan
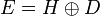
Il existe une droite $D$ telle que $E=H \oplus D$
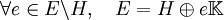
$\forall e \in E \backslash H, \quad E=H \oplus e \mathbb{K}$

Représentation des sous-espaces

Soit F un sous-espace vectoriel de dimension finie.

On peut représenter ce sous-espace comme une intersection finie d'hyperplans indépendants. Ce théorème est détaillé dans l'article espace dual.

v · d · m Algèbre linéaire générale
Vecteur • Scalaire • Combinaison linéaire • Espace vectoriel • Matrice
Famille de vecteurs	Famille génératrice • Famille libre (indépendance linéaire) • Base • Théorème de la base incomplète • Rang • Colinéarité
Sous-espace	Sous-espace vectoriel • Somme d'ensembles • Somme directe • Sous-espace supplémentaire • Dimension • Codimension • Droite • Plan • Hyperplan
Morphisme et notions relatives	Application linéaire • Noyau • Conoyau • Lemme des noyaux • Pseudo-inverse • Théorème de factorisation • Théorème du rang • Équation linéaire • Système d'équations linéaires • Élimination de Gauss-Jordan • Forme linéaire • Espace dual • Orthogonalité • Base duale • Endomorphisme linéaire • Valeur propre, vecteur propre et espace propre • Spectre • Projecteur • Symétrie • Matrice diagonalisable • Diagonalisation • Endomorphisme nilpotent
En dimension finie	Espace vectoriel de dimension finie • Trace • Déterminant • Polynôme caractéristique • Polynôme d'endomorphisme • Théorème de Cayley-Hamilton • Polynôme minimal d'un endomorphisme • Invariants de similitude • Réduction d'endomorphisme • Réduction de Jordan • Décomposition de Dunford • Décomposition de Frobenius
Enrichissements de structure	Norme • Produit scalaire • Forme quadratique • Espace vectoriel topologique • Orientation • Algèbre sur un corps • Algèbre de Lie • Complexe différentiel
Développements	Théorie des matrices • Représentation de groupe • Analyse fonctionnelle • Algèbre multilinéaire • Module sur un anneau

Exemples

- Introduction - Définition - Lien avec les formes linéaires - Caractérisation - Représentation des sous-espaces - Exemples

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️

Le régime cétogène montre des surprises sur le cholestérol 🧐

Un tango observationnel révèle une Super-Terre 🔭

Cette expérience montre que la graisse brune augmente fortement la longévité 🕒

L'Univers comme jamais vu auparavant: les révélations du fond diffus cosmologique 🔭

C'est sérieux: de la bave pourrait révolutionner la conception de bioplastiques 🪱

Découverte: le trou noir central de notre galaxie pourrait anéantir la vie sur Terre 💥

Etude scientifique: ces aliments nous font vieillir 🍽️

Pourquoi notre visage est-il plus petit et délicat que celui des Néandertaliens ? 🤔

A 18 ans, il découvre 1,5 million d'objets célestes inconnus avec son algorithme d'IA 🌟

Que sont ces objets rouges et aplatis, qualifiés d'UFOs par les astronomes ? 🔭

Une méthode simple pour améliorer les performances en mathématiques 🧮

Que sont ces étranges éclairs rouges photographiés au-dessus de l'Himalaya ? ⚡

Nous descendons non pas d'un, mais d'au moins deux groupes anciens 🧬

Un nuage géant de 160 000 soleils découvert dans notre Voie lactée 🔭

Connaissez-vous le rat-kangourou musqué, ce marsupial à la démarche unique ? 🦘

Comment une poignée de traders a fait s'effondrer deux cryptomonnaies 📉

Première cartographie titanesque d'un cerveau, avec 500 millions de connexions neuronales 🧠

Cette double supernovae proche est inexorable, voici la date... qui va vous surprendre 💥

Un océan phosphorescent: comment s'explique ce phénomène rare et féerique ? 🌊

L'ELT pourrait-il découvrir une vie extraterrestre dès 2028 ? 🔭

Cet édulcorant tue les superbactéries résistantes 🍬

Les neutrinos, la clé de la gravité quantique ? 👀

En Italie, les éruptions explosives de ce volcan déjouent les pronostics 🌋

Que sont ces spaghettis au cœur de notre galaxie ? 🔭

Des scientifiques ont créé une "bombe intelligente" contre le cancer 🎯

Les nanoplastiques, l'amiante du 21ème siècle ? 🔬

Compétition cellulaire: des forces sculptent nos tissus 🛠️

Le climat en Europe et au États-Unis pourrait changer bien plus radicalement que supposé 🌍

Découverte: ce dinosaure avait des poches d'air dans les os 🦴

La vie sur Titan, si elle existe, ressemblerait à quoi ? 🪐

Magnétisme et biologie s'allient contre le cancer 🧲

WR 104: on en sait plus sur cette "étoile de la mort" qui menace la Terre ☄️

Découverte: des bactéries respiraient de l'oxygène 1 milliard d'années avant la Grande Oxydation 🫧

Découverte d'un nouveau type de vent solaire rapide ☀️

Les dinosaures n'étaient pas en déclin avant l'astéroïde 🦖

Ce robot-cheval est véritablement tout-terrain 🐎

Comment un mauvais sommeil peut endommager votre cerveau ? 🧠

Découverte de microbes cachés qui purifient l'eau sans que nous le sachions 💧

Bonne nouvelle pour les enfants de la Lune 🌙

Du CO2 détecté dans l'atmosphère d'une exoplanète proche 🔭

Le café et le thé impactent le cancer, mais dans quel sens ? ☕

Une IA révèle des bulles cosmiques dans notre galaxie 🫧

Lorsque l'alcool stimule ses phéromones sexuelles et rend plus séduisant 🍷

Page générée en 0.139 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise