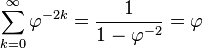Base d'or - Définition
La liste des auteurs de cet article est disponible ici.
Non-unicité
Comme avec tout système de numération de base n, les nombres dont le développement est fini peuvent s'écrire de plusieurs façons. En base 10, cela est relié à l'observation suivante : si x = 0,9999... alors 10x = 9,99999... donc 9x = 9 et x = 1. En base

- Conversion d'une forme non-standard :
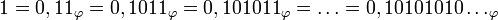
- Série géométrique : 1,0101010

- Différence entre deux « déplacements » :
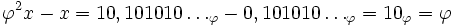
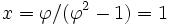
Cette non-unicité est une spécificité du système de numération, puisque 1,0000 et 0,101010... sont tous les deux dans la forme standard.
Représenter les entiers sous forme de nombres en base d'or
Nous pouvons, soit considérer nos entiers comme étant les (seuls) chiffres d'une base

Notez que :
-
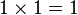
-
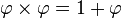
-
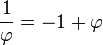
Par conséquent, nous pouvons calculer
-
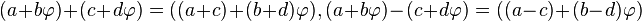
et
-
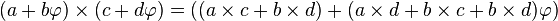
Ainsi, en utilisant les valeurs entières seulement, nous pouvons ajouter, soustraire et multiplier des nombres de la forme
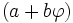

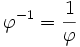
 si et seulement si
si et seulement si  . Si un côté est négatif, l'autre côté est positif, la comparaison est triviale. Autrement, élever au carré les deux côtés, pour obtenir une comparaison entière, renverser la comparaison si les deux côtés étaient négatifs. Lors de l'élévation au carré des deux côtés,
. Si un côté est négatif, l'autre côté est positif, la comparaison est triviale. Autrement, élever au carré les deux côtés, pour obtenir une comparaison entière, renverser la comparaison si les deux côtés étaient négatifs. Lors de l'élévation au carré des deux côtés,
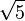
Ainsi, en utilisant les valeurs entières seulement, nous pouvons aussi comparer les nombres de la forme
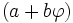
- Pour convertir un entier x en un nombre en base-

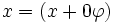
- Soustraire la plus haute puissance de


- Jusqu'à ce que notre nombre soit 0, aller à l'étape 2.
- Fini.
La procédure ci-dessus ne donnera jamais la suite « 11 », puisque
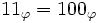
C’est-à-dire : démarrons avec l'entier 5, le résultat étant
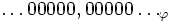
La plus haute puissance de
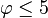
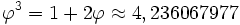
En soustrayant ceci de 5, nous avons
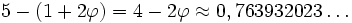
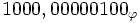
La plus haute puissance de
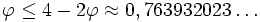
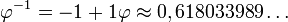
En soustrayant ceci de
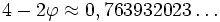
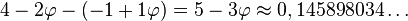
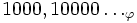
La plus haute puissance de
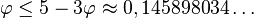
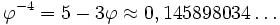
En soustrayant ceci de
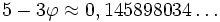
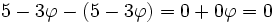
-
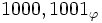
Addition, soustraction et multiplication
Il est possible d'adapter tous les algorithmes standards de l'arithmétique de la base 10 pour l'arithmétique de la base

Calculer puis convertir en forme standard
Pour l'addition de deux nombres en base

Par exemple
- 2+3 = 10,01 + 100,01 = 110,02 = 110,1001 = 1000,1001
- 2×3 = 10,01 × 100,01 = 1000,1 + 1,0001 = 1001,1001 = 1010,0001
- 7-2 = 10000,0001 - 10,01 = 10010,0101 = 1110,0101 = 1001,0101 = 1000,1001
Éviter les chiffres autres que 0 et 1
Une approche plus « naïve » est d'éviter d'avoir à ajouter les chiffres 1+1 ou soustraire 0-1. Ceci est réalisé en réorganisant les opérandes en forme non-standard pour que ces combinaisons n'apparaissent pas. Par exemple
- 2+3 = 10,01 + 100,01 = 10,01 + 100,0011 = 110,0111 = 1000,1001
- 7-2 = 10000,0001 - 10,01 = 1100,0001 - 10,01 = 1011,0001 - 10,01 = 1010,1101 - 10,01 = 1000,1001
La soustraction vue ici utilise une forme modifiée de l'algorithme d'échange standard pour la soustraction.