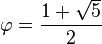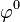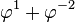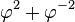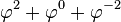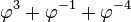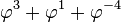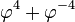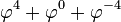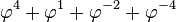Base d'or - Définition

Introduction

En mathématiques, le nombre d'or, à savoir

peut être utilisé comme une base de numération. Ce système est connu sous le nom base d'or, ou accessoirement, phinaire (car le symbole pour le nombre d'or est la lettre grecque « phi »). Tout nombre réel possède une représentation standard en base où seuls les chiffres 0 et 1 sont utilisés, et où la suite « 11 » est évitée. Une base non-standard avec cette suite de chiffre (ou avec d'autres chiffres) peut toujours être réécrite en forme standard, la reliant aux propriétés algébriques du nombre — c’est-à-dire que . Par exemple . Malgré l'usage d'une base irrationnelle, c'est un fait remarquable que tous les nombres entiers possèdent une représentation unique en développement fini dans la base . Les autres nombres possèdent des représentations standards en base , les nombres rationnels ayant des représentations récurrentes. Ces représentations sont uniques, excepté celles des nombres qui ont un développement fini ainsi qu'un développement non-fini (de la même manière qu'en base 10 : 2,2=2,199999...)

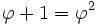
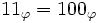
Ramener un nombre en base φ à sa forme standard

Écritures en base φ

Décomposition (standard) des neuf premiers entiers

Entier	Puissances de	Base
1		1
2		10,01
3		100,01
4		101,01
5		1000,1001
6		1010,0001
7		10000,0001
8		10001,0001
9		10010,0101

En s'inspirant de l'écriture décimale positionnelle, la notation x=211,01_φ désignera le nombre

x = 2φ² + 1φ¹ + 1φ⁰ + 0φ ^{− 1} + 1φ ^{− 2} = 2φ² + φ + 1 + φ ^{− 2}

Avec cette convention, le nombre d'or lui même est noté 10_φ, son carré est 100_φ, son inverse 0,1_φ.

Le nombre d'or vérifie par définition la relation algébrique φ²=φ+1, ce qui permet de réécrire le nombre x sous d'autres formes, comme

x = φ² + (φ² + φ) + 1 + φ ^{− 2} = φ³ + φ² + 1 + φ ^{− 2} = 1101,01_φ

Le même nombre peut donc avoir plusieurs écritures phinaires : la première écriture de x a fait intervenir les chiffres 0,1,2 ; la seconde n'utilise plus que 0 et 1. Il n'y a pas de raison a priori de se limiter à des chiffres allant de 0 à 9, on pourrait noter par exemple

y = 23[18]5,0[12]_φ pour

y = 2φ³ + 3φ² + 18φ + 5 + 12φ ^{− 2}

Avec 12 et 18 vus comme des chiffres dans l'écriture phinaire de y.

Principe de la standardisation

Tout nombre réel possède une représentation standard en base où seuls les chiffres 0 et 1 sont utilisés, et où on ne trouve jamais la séquence de chiffres « 11 ». Le tableau ci-contre donne des représentations standard pour les premiers nombres entiers.

Un nombre écrit sous forme phinaire non standard peut toujours être réécrit sous forme standard, en usant judicieusement de la formule φ + 1 = φ². Par exemple le nombre φ² lui-même peut être écrit 11_φ sous forme non standard, 100_φ sous forme standard.

Le nombre 211,01_φ n'est pas une écriture standard, puisqu'il contient le chiffre « 2 », et il contient en outre une séquence de chiffres « 11 ». Pour standardiser ce chiffre, nous pouvons utiliser les substitutions suivantes :

• la séquence de chiffres « 011 » peut être réécrite « 100 », ce qui exprime la relation φ + 1 = φ²
• la séquence « 0200 » peut se réécrire « 1001 », par application de la relation 2φ² = φ³+1

À chaque fois qu'on décèle dans l'écriture de x un motif interdit (011 ou 0200), on applique une de ces substitutions, et on répète l'opération jusqu'à disparition de ces motifs. Quel que soit l'ordre dans lequel on procède, le résultat sera le même : le nombre x écrit sous forme standard. La recherche des motifs est à comprendre au sens large : ainsi le motif « 0410 » contient à la fois le motif « 011 » (0410 = 0300+0110) et le motif « 0200 » (0410=0200+0210).

Voici avec l'exemple du nombre x=211,01_φ les substitutions utilisées (à droite), et les écritures phinaires successives de ce nombre

        211,01φ        300,01φ     011φ → 100φ       1101,01φ     0200φ → 1001φ      10001,01φ     011φ → 100φ       

Prise en compte des chiffres négatifs

Il est possible de prendre pour chiffres d'une écriture phinaire des entiers négatifs. Ainsi le nombre 211,0[-1]_φ n'est pas une écriture standard, puisqu'il contient les chiffres « -1 » et « 2 », qui ne sont pas « 0 » ou « 1 » ; il contient en outre une séquence de chiffres « 11 ».

Pour standardiser ce chiffre, nous pouvons ajouter aux substitutions précédentes une nouvelle opération : 0[-1]0_φ → [-1]01_φ issue de -φ = -φ²+1. Pour alléger l'écriture le signe « - » sera porté au-dessous du chiffre auquel il s'applique : cette substitution sera ainsi notée

010_φ → 101_φ.

Voici le résultat de l'application de l'algorithme pour le nombre considéré

        211,01φ        300,01φ     011φ → 100φ       1101,01φ     0200φ → 1001φ      10001,01φ     011φ → 100φ (de nouveau)      10001,101φ    010φ → 101φ      10000,011φ    010φ → 101φ (de nouveau)      10000,1φ      011φ → 100φ (de nouveau)      

À la fin de l'algorithme, le seul chiffre pouvant encore valoir « -1 » est le premier terme. Précisément, le signe du nombre x est justement le signe de son premier chiffre.

Tout nombre positif représenté en base non-standard peut être standardisé de manière unique de cette façon. Si le nombre est négatif, on peut à la fin de cette première standardisation mettre le signe moins en facteur, ce qui revient à changer chaque chiffre en son opposé, et réappliquer l'algorithme au résultat. On aura alors l'opposé d'un nombre positif écrit sous forme standardisée.

Si cette arithmétique est exécutée par un ordinateur, un message d'erreur peut apparaître.