Arithmétique - Définition

Introduction

L'arithmétique est une branche des mathématiques qui comprend la partie de la théorie des nombres qui utilise des méthodes de la géométrie algébrique et de la théorie des groupes. On l'appelle plus généralement la « science des nombres ». Son étymologie provient du mot grec « αριθμός » qui signifie « nombre ».

Autrefois, l'arithmétique se limitait à l'étude des propriétés des entiers naturels, des entiers relatifs, et des nombres rationnels (sous forme de fractions), et aux propriétés des opérations sur ces nombres.

Les opérations arithmétiques traditionnelles sont l'addition, la division, la multiplication, et la soustraction.

Cette discipline fut ensuite élargie par l'inclusion de l'étude d'autres nombres comme les réels (sous forme de développement décimal illimité), ou même de concepts plus avancés, comme l'exponentiation ou la racine carrée.

Histoire

Dans l'école pythagoricienne (Pythagore de Samos), à la deuxième moitié du VI^e siècle avant J.-C., l'arithmétique était, avec la géométrie, l'astronomie et la musique, une des quatre sciences quantitatives ou mathématiques (Mathemata). Celles-ci furent regroupées au sein des sept arts libéraux par Martianus Capella (V^e siècle), et plus précisément désignées sous le nom de quadrivium par Boèce. Les trois autres disciplines étaient littéraires (grammaire, rhétorique, dialectique) et firent l'objet des travaux de Cassiodore et, plus tard, Alcuin qui leur donna le nom de trivium.

Ensembles utilisés en arithmétique

La totalité des nombres ont été regroupés dans des ensembles. Les plus connus sont :

•  : l'ensemble des entiers naturels ( ).
•  : l'ensemble des entiers relatifs ( ).
•  : l'ensemble des nombres décimaux, c'est-à-dire qui s'écrivent sous la forme d'un quotient d'un nombre entier relatif et d'une puissance positive de 10, c'est-à-dire, où x est un nombre entier relatif et n un nombre entier naturel .
•  : l'ensemble des nombres rationnels, c'est-à-dire des nombres pouvant s'écrire comme un quotient (résultat d'une division) de deux nombres entiers relatifs. En posant la division, il peut y avoir une infinité de chiffres après la virgule dans le résultat, mais ces chiffres finiront par se répéter; dans ce cas on dit que l'écriture décimale est illimitée périodique. .
•  : l'ensemble des nombres réels, mesurant toutes les distances entre deux points d'une droite, peuvent se voir comme limite de nombres rationnels, peuvent s'écrire avec des chiffres après la virgule mais les chiffres ne se répètent plus nécessairement (π, le nombre d'or, ).
•  : nombres complexes de la forme x + iy où x et y sont réels et i imaginaire tel que i² = − 1.

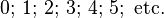
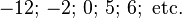
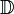
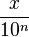
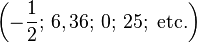
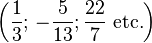
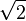
Certains de ces ensembles sont des sous-ensembles des autres ; Tous les éléments de appartiennent aussi à , par exemple. Mais à l'inverse, un élément de n'est pas forcément élément de . On peut représenter ces ensembles par des cercles concentriques: le plus petit est , puis viennent , , , et .

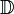
Il est possible de ne considérer qu'une partie d'un ensemble. Ainsi, on notera l'ensemble des nombres positifs de . De même on notera l'ensemble privé de 0. On remarque entre autres que et que (il s'agit de « privé de » .).

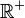
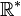
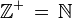
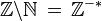
Différentes arithmétiques

Arithmétique élémentaire

L'expression arithmétique élémentaire désigne parfois la forme la plus basique des mathématiques, apprise à l’école élémentaire. Il s’agit essentiellement de l’étude des nombres, et des opérations élémentaires (soustraction, addition, division, multiplication).

Ce terme désigne aussi les rudiments des techniques de l'arithmétique. Les outils utilisés sont la division euclidienne, le lemme d'Euclide, le théorème de Bachet-Bézout ou encore le théorème fondamental de l'arithmétique. Il permet de démontrer des théorèmes comme celui de Wilson ou encore le petit théorème de Fermat.

Cette deuxième acception du terme est traité dans l'article détaillé.

Arithmétique modulaire

Carl Friedrich Gauss étudie l'ensemble des congruences sur les entiers, c'est-à-dire celui composé des restes de la division euclidienne par un nombre entier donné. Cet ensemble est naturellement muni d'une addition et d'une multiplication.

L'étude de cette structure porte le nom d'arithmétique modulaire. Elle permet de généraliser les résultats de l'arithmétique élémentaire. Le théorème d'Euler, correspondant à un résultat plus fort que celui du petit théorème de Fermat, illustre une généralisation.

L'arithmétique modulaire est utilisé en cryptologie ou pour la construction de codes correcteurs en informatique.

Théorie algébrique des nombres

De nombreuses questions ne trouvent pas de réponse, même avec les techniques de l'arithmétique modulaire. Des exemples proviennent d'équations diophantiennes, c'est-à-dire d'équations dont les coefficients sont entiers et dont les solutions recherchées sont entières. Une méthode consiste à élargir l'ensemble des entiers à une nouvelle structure qualifiée d'anneau d'entiers algébriques, comme ceux des entiers de Gauss, d'Eisenstein ou ceux associés aux nombres de la forme a + b.√5 définissant une arithmétique du nombre d'or.

L'étude de cette structure, plus générale que celle de l'arithmétique modulaire qui se limite aux anneaux euclidiens, constitue le premier chapitre de la théorie algébrique des nombres.

Arithmétique des polynômes

L'étude de l'arithmétique, au sens des nombres entiers, suppose d'établir des théorèmes. Ces théorèmes se démontrent à l'aide de techniques qui ne se limitent pas aux nombres entiers. Il est possible de faire usage de la même démarche sur d'autres structures, comme par exemple celle des polynômes. A travers l'étude des polynômes cyclotomiques, Gauss parvient à trouver un nouveau polygone régulier constructible à la règle et au compas, de 17 côtés.

Sa démarche est de nature arithmétique, pour cette raison, on parle d'arithmétique des polynômes.