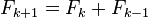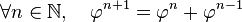Base d'or - Définition
La liste des auteurs de cet article est disponible ici.
Représenter les rationnels sous forme de nombres en base d'or
Chaque nombre rationnel peut être représenté sous forme de développement en base

![\mathbb{Q}[\sqrt 5] = \mathbb{Q} + \mathbb{Q}[\sqrt 5]\,](https://static.techno-science.net/illustration/Definitions/autres/7/7a2fdd2007eda280cc15d91cb25954d1_021d3756216a7abf2c392348f02adfcf.png)
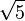

![\mathbb{Q}[\sqrt 5]\,](https://static.techno-science.net/illustration/Definitions/autres/4/4ee65fcd22f8e73129b9b7f8f22bfd7d_ca46e470b77a9580addf84837b95b652.png)
-

-

-
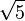
-
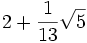
La justification qu'un rationnel donne un développement répétitif est analogue à la démonstration équivalente pour un système de numération en base n (n = 2, 3, 4,...). Essentiellement pour les longues divisions en base

.0 1 0 0 1 ------------------------ 1 0 0 1 ) 1 0 0.0 0 0 0 0 0 0 0 1 0 0 1 échange: 10000 = 1100 = 1011 ------- donc 10000-1001 = 1011-1001 = 10 1 0 0 0 0 1 0 0 1 ------- etc.
La réciproque est également vraie, vu qu'un nombre représenté en base

![\mathbb{Q}[\sqrt 5]\,](https://static.techno-science.net/illustration/Definitions/autres/4/4ee65fcd22f8e73129b9b7f8f22bfd7d_ca46e470b77a9580addf84837b95b652.png)
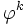
![\mathbb{Q}[\sqrt 5]\,](https://static.techno-science.net/illustration/Definitions/autres/4/4ee65fcd22f8e73129b9b7f8f22bfd7d_ca46e470b77a9580addf84837b95b652.png)
Une relation étroite : représentation de Fibonacci
Un système de numération en relation étroite est la représentation de Fibonacci utilisée pour les entiers. Dans ce système, seuls les chiffres 0 et 1 sont utilisés et les valeurs des places de ces chiffres sont les nombres de Fibonacci. Puisqu'avec une base

Par exemple :
-
- 30 = 1×21 + 0×13 + 1×8 + 0×5 + 0×3 + 0×2 + 1×1 + 0×1 = 10100010fib.
Cette relation de récurrence est à rapprocher de celle qui relie les puissances du nombre d'or

Division
Aucune fraction (a/b, où a et b sont des nombres entiers, a non divisible par b) ne peut être représenté comme un nombre fini en base


![\mathbb{Q}[\sqrt 5]](https://static.techno-science.net/illustration/Definitions/autres/6/6d03ee8b68ac69b84aef623d36ca56bd_1d6d3ae256548f826e4776dcb48e3498.png)