Cardinal mesurable - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définitions et propriétés de grand cardinal - Mesures à valeurs réelles - Cardinaux mesurables, ultraproduits, et théorie des modèles

Introduction

En mathématiques, un cardinal mesurable est un cardinal sur lequel existe une mesure définie pour tout sous-ensemble ; cette propriété fait qu'un tel cardinal est un grand cardinal.

Définitions et propriétés de grand cardinal

Un cardinal mesurable est un cardinal non dénombrable κ tel qu'il existe une mesure μ non-triviale, κ-additive, à valeurs dans ${0,1}$ , définie sur tous les sous-ensembles de κ ; μ est donc une application de l'ensemble des parties de κ vers ${0,1}$ telle que :

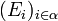
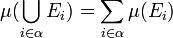
Pour toute famille $(E_i)_{i\in\alpha}$ (avec α<κ) de sous-ensembles disjoints de κ, on a $\mu(\bigcup_{i\in\alpha}E_i)=\sum_{i\in\alpha}\mu(E_i)$ ;
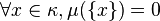
$μ(κ) = 1$ et $\forall x\in \kappa, \mu(\{x\})=0$ .

Cela revient à dire qu'il existe sur κ un ultrafiltre U (formé des sous-ensembles de mesure 1), non trivial et <κ-additif, c'est-à-dire que l'intersection de toute famille de α éléments de U (avec α<κ) est encore dans U, ou encore que la réunion de toute famille de α éléments non dans U n'appartient pas non plus à U. Les cardinaux mesurables furent introduits en 1930 par Stanislaw Ulam, qui montra que le plus petit cardinal κ possédant une mesure (complète) dénombrablement additive devait en fait posséder une mesure κ-additive.

Si κ est un cardinal mesurable, on démontre qu'il existe sur κ une mesure normale ν, c'est-à-dire une mesure telle que pour toute application f:κ→κ telle que f(α)<α pour presque tous les α<κ, il existe un β<κ tel que f(α)=β pour presque tous les α<κ ("presque tous" étant entendu au sens de la mesure ν). Les constructions d'ultraproduits qui seront exposées dans la prochaine section utilisent des mesures normales.

Sans l'axiome du choix, il est parfaitement possible qu'un cardinal mesurable soit un successeur, et l'axiome de détermination (en) entraîne même que ω₁ est un cardinal mesurable. En revanche, l'axiome du choix implique que tout cardinal mesurable est inaccessible.

On voit facilement que si κ admet une mesure κ-additive non triviale, κ doit être régulier : tout sous-ensemble de cardinal < κ doit être de mesure nulle, et par κ-additivité, cela implique que κ ne peut pas être union de moins de κ ensembles de cardinalité inférieure à κ.

Supposons alors que λ < κ ; montrons qu'on ne peut avoir κ ≤ 2^λ. Dans le cas contraire, on pourrait identifier κ avec un ensemble de suites de 0 et de 1 de longueur λ. Pour chaque indice d'une telle suite, le sous-ensemble des suites ayant 1 à cette position ou celui ayant 0 à cette position serait de mesure 1. L'intersection de ces λ sous-ensembles de mesure 1 serait ainsi également de mesure 1(par κ-additivité), mais cette intersection contient exactement une suite, ce qui contredirait la non-trivialité de la mesure. Ainsi, admettant l'axiome du choix (sans lequel on n'a pas forcément un ordre total entre cardinaux), on voit que λ < κ implique 2^λ<κ, et donc que κ est un cardinal (fortement) limite, ce qui complète la démonstration.

On voit ainsi qu'un axiome de grand cardinal peut n'avoir ce statut que par rapport à un système donné. La section suivante montrera en fait que, toujours en admettant l'axiome du choix (ce que nous ferons désormais sans le préciser), un cardinal mesurable est Mahlo, Ramsey (en), etc.

Mesures à valeurs réelles

On dit qu'un cardinal κ est mesurable (à valeurs réelles) s'il existe une mesure non-atomique (à valeurs réelles) κ-additive sur l'ensemble des parties de κ. L'hypothèse du continu (à savoir ${\mathfrak c}=2^{\aleph_0}$ ) implique que ${\mathfrak c}$ n'est pas mesurable à valeurs réelles ; d'autre part, tout cardinal mesurable (à valeurs réelles) est faiblement Mahlo (en). Solovay a montré que (dans ZFC) l'affirmation de l'existence de cardinaux mesurables et celle de l'existence de cardinaux mesurables à valeurs réelles sont des axiomes équicohérents.