Codage de Rice - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le codage de Rice, codage de Golomb-Rice ou GPO2 (pour Golomb-power-of-2) est un codage entropique inventé par Robert F. Rice et James R. Plaunt en 1971 et utilisé essentiellement en compression de données.
Le code produit est un code préfixe.
Principe
Le codage de Rice d'un entier naturel N dépend d'un paramètre k et se fait en deux étapes :
- le codage du quotient de la division euclidienne de N par 2k avec un codage unaire ;
- le codage du reste de la même division avec un codage binaire.
Le codage de Rice de paramètre k est strictement équivalent à un codage de Golomb de paramètre 2k.
Mathématiquement, pour coder un entier
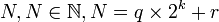
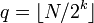
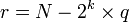
La division par 2k peut être implémentée par un décalage de k bits vers la droite, et la second étape revient à répliquer les k bits de poids faible de la valeur à coder. Ces opérations simples font que le codage de Rice est particulièrement adapté pour une implémentation rapide.
Optimalité
Le codage de Rice est adapté pour des données dans lesquelles les valeurs les plus faibles sont plus probables que les autres (mais où les autres peuvent malgré tout apparaitre).
Il est particulièrement apprécié en informatique car son implémentation est simple est rapide.
Exemples
| Décimal | Binaire | Code de Rice k = 0 | Code de Rice k = 1 | Code de Rice k = 2 | Code de Rice k = 3 | Code de Rice k = 4 |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 0 | 0 00 | 0 000 | 0 0000 |
| 1 | 0001 | 10 | 0 1 | 0 01 | 0 001 | 0 0001 |
| 2 | 0010 | 110 | 10 0 | 0 10 | 0 010 | 0 0010 |
| 3 | 0011 | 1110 | 10 1 | 0 11 | 0 011 | 0 0011 |
| 4 | 0100 | 11110 | 110 0 | 10 00 | 0 100 | 0 0100 |
| 5 | 0101 | 111110 | 110 1 | 10 01 | 0 101 | 0 0101 |
| 6 | 0110 | 1111110 | 1110 0 | 10 10 | 0 110 | 0 0110 |
| 7 | 0111 | 11111110 | 1110 1 | 10 11 | 0 111 | 0 0111 |
| 8 | 1000 | 111111110 | 11110 0 | 110 00 | 10 000 | 0 1000 |
| 9 | 1001 | 1111111110 | 11110 1 | 110 01 | 10 001 | 0 1001 |
| 10 | 1010 | 11111111110 | 111110 0 | 110 10 | 10 010 | 0 1010 |
Choix du paramètre
Le choix du paramètre k utilisé lors du codage de Rice détermine le taux de compression qu'il est possible d'obtenir.
Le paramètre optimal kopt pour coder V valeurs sur un intervalle de taille I est exprimé par :
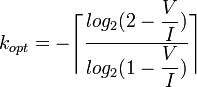
Utilisations
Le codage de Rice fait partie des codages entropiques les plus utilisés, lorsque les données à compresser présentent une distribution géométrique (ou approchante) et que la vitesse de l'algorithme est un critère important.
On le retrouve notamment dans de nombreux algorithmes de compression multimédia : audio (FLAC, Monkey's Audio, MPEG-4 ALS, ALAC...), vidéo, image... et dans certains algorithmes de compression d'index (pour les moteurs de recherche).

















































