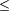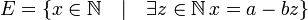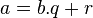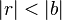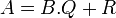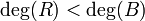Division euclidienne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en arithmétique, la division euclidienne ou division entière est une opération qui, à deux entiers naturels appelés dividende et diviseur, associe deux entiers appelés quotient et reste. Initialement définie pour deux entiers naturels non nuls, elle se généralise aux entiers relatifs et aux polynômes, par exemple.
Cette division est à la base des théorèmes de l'arithmétique élémentaire, comme celle de l'arithmétique modulaire qui donne lieu à la création des congruences sur les entiers.
Définitions
Division euclidienne dans les entiers positifs
Le théorème de division euclidienne pour des entiers positifs s'énonce ainsi : pour tous entiers a et b positifs, avec b non nul, il existe un unique couple d'entiers q et r tel que la relation a=bq+r soit vérifiée, et tel que r soit compris entre 0 et b-1 au sens large. L'entier q est appelé quotient de la division de a par b, et l'entier r reste de cette division.
Soient a et b deux entiers positifs, avec b non nul.
- Existence
Considérons l'ensemble E défini par :
E est non vide car il contient a. Comme E est une partie non vide de N, par axiome, le minimum de E existe. Notons r ce minimum et q l'entier qui le définit, c’est-à-dire celui vérifiant l'égalité a - b.q = r, Par construction r est un entier naturel. L'entier r - b ne peut être élément de E et donc est strictement négatif, ce qui montre que r est strictement plus petit que b. L'existence est alors démontrée.
- Unicité
Division euclidienne dans les entiers relatifs
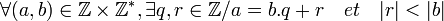
À deux entiers a et b, avec b non nul, la division euclidienne associe un quotient q et un reste r, tout deux entiers, vérifiant :
L'affirmation de l'existence du reste et du quotient est appelée Théorème de la division euclidienne pour les entiers.
S'il était possible de définir une division telle que l'unicité du quotient et du reste soit garantie, elle serait néanmoins incompatible avec le cas général de la division dans les anneaux euclidiens.
La définition de la division euclidienne sur les entiers naturels permet de prouver l'existence de deux entiers naturels q1 et r1 tels que
- | a | = | b | q1 + r1 avec r1 < | b |
Une petite étude sur les signes respectifs de a et b permet de donner pour la division euclidienne de a par b
- pour a et b négatifs , quotient q1 et reste - r1
- pour a négatif et b positf , quotient - q1 et reste - r1
- pour a positif et b négatif , quotient - q1 et reste r1
- Pour a et b positifs, quotient q1 et reste r1
Division euclidienne dans l'ensemble des polynômes
La division euclidienne selon les puissances décroissantes existe si l'anneau est défini sur un corps :
![\forall (A,B)\in\mathbb{K}[X]\times\mathbb{K}[X]^*,\quad \exists !Q, R\in\mathbb{K}[X], A=B.Q+R \quad avec \quad \operatorname{deg}(R) < \operatorname{deg}(B)](https://static.techno-science.net/illustration/Definitions/autres/2/2630f301bb91125be04dbf453fc1749b_a43f160575b6df512a499c7c2ec0d3f9.png)
À deux polynômes A et B à coefficients dans un corps K avec B non nul, la division euclidienne associe un unique quotient Q et un unique reste R, tout deux polynômes, vérifiant :
L'unicité est ici garantie, en revanche il est nécessaire que K soit un corps. Sinon la division est encore parfois possible, si par exemple le coefficient du monôme dominant de B est égal à 1, ou plus généralement si le coefficient du monôme dominant de B est inversible.
Division euclidienne dans un anneau
Dans certains types d'anneaux commutatifs unitaires intègres, on peut définir une division euclidienne par
- a = bq + r avec r = 0 où v(r) < v(b) v étant une application de A - { 0 } dans

S'il existe un stathme euclidien sur l'anneau A, il en existe un qui vérifie la propriété suivante : si a et b sont deux éléments de A tel que b divise a, alors v(b)