Codage de Golomb - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le codage de Golomb est un codage entropique inventé par Solomon Wolf Golomb en 1966 et utilisé essentiellement en compression de données.
Le code produit est un code préfixe.
Principe
Le codage de Golomb d'un entier naturel N dépend d'un paramètre k et se fait en deux étapes :
- le codage du quotient de la division euclidienne de N par k avec un codage unaire ;
- le codage du reste de la même division avec un codage binaire tronqué.
Mathématiquement, pour coder un entier
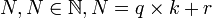
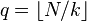
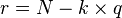
Optimalité
Le codage de Golomb est adapté pour des données dans lesquelles les valeurs les plus faibles sont plus probables que les autres (mais où les autres peuvent malgré tout apparaitre).
Utilisations
Le codage de Golomb est principalement utilisé dans sa variante dite codage de Rice qui peut être implémentée de façon plus efficace. Un codage de Rice est d'ailleurs équivalent à un codage de Golomb dont le paramètre est 2 élevé à la puissance du paramètre de Rice.
Exemples
| Décimal | Binaire | Code de Golomb k = 1 (unaire) | Code de Golomb k = 2 | Code de Golomb k = 3 | Code de Golomb k = 4 | Code de Golomb k = 5 | Code de Golomb k = 10 | Code de Golomb k = 16 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0000 | 0 | 0 0 | 0 0 | 0 00 | 0 00 | 0 000 | 0 0000 |
| 1 | 0001 | 10 | 0 1 | 0 10 | 0 01 | 0 01 | 0 001 | 0 0001 |
| 2 | 0010 | 110 | 10 0 | 0 11 | 0 10 | 0 10 | 0 010 | 0 0010 |
| 3 | 0011 | 1110 | 10 1 | 10 0 | 0 11 | 0 110 | 0 011 | 0 0011 |
| 4 | 0100 | 11110 | 110 0 | 10 10 | 10 00 | 0 111 | 0 100 | 0 0100 |
| 5 | 0101 | 111110 | 110 1 | 10 11 | 10 01 | 10 00 | 0 101 | 0 0101 |
| 6 | 0110 | 1111110 | 1110 0 | 110 0 | 10 10 | 10 01 | 0 1100 | 0 0110 |
| 7 | 0111 | 11111110 | 1110 1 | 110 10 | 10 11 | 10 10 | 0 1101 | 0 0111 |
| 8 | 1000 | 111111110 | 11110 0 | 110 11 | 110 00 | 10 110 | 0 1110 | 0 1000 |
| 9 | 1001 | 1111111110 | 11110 1 | 1110 0 | 110 01 | 10 111 | 0 1111 | 0 1001 |
| 10 | 1010 | 11111111110 | 111110 0 | 1110 10 | 110 10 | 110 00 | 10 000 | 0 1010 |

















































