Code correcteur - Définition
La liste des auteurs de cet article est disponible ici.
Redondance et fiabilité
Distance de Hamming
Le concept le plus utilisé pour la modélisation de la redondance est celui de la distance de Hamming. À deux mots du code, elle associe le nombre de lettres qui diffèrent.
- La distance de Hamming entre "ramer" et "cases" est 3.
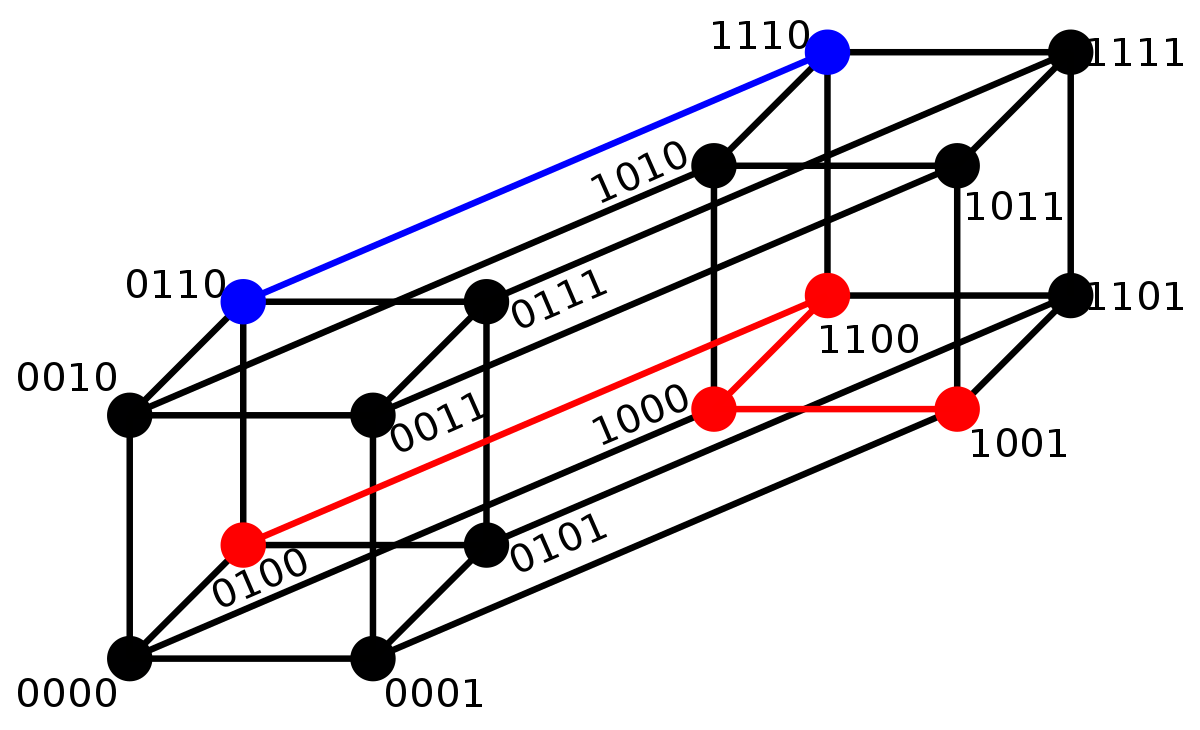
La figure de droite illustre le cas où les lettres de l'alphabet sont binaires et la dimension du code égale à quatre. La distance entre 0110 et 1110 est égale à un car il est nécessaire de parcourir un segment du graphique pour joindre les deux mots. On peut aussi remarquer que les deux mots diffèrent seulement par leur première lettre. La même approche montre que la distance entre 0100 et 1001 est égale à trois.
Ce concept permet la définition suivante :
-
- La distance minimale d'un code correcteur est la plus petite distance au sens de Hamming entre deux mots du code.
Cette définition permet de formaliser les trois paramètres les plus important d'un code en blocs.
-
- Les paramètres d'un code en blocs sont la longueur du code n, le nombre M de mots du code et la distance minimale δ. Ils sont en général noté {n, M, δ}
Code parfait
Usuellement, on considère que le mot de code émis est celui se trouvant le plus près du mot reçu, ce qui revient à supposer que le minimum de lettres a été modifié. Ce procédé conduit à une erreur de décodage chaque fois que l'erreur est supérieure à la capacité corrective du code. La question naturelle est celle de la valeur de t correspondant au nombre maximum d'erreurs corrigibles.
Une interprétation géométrique donne un élément de réponse. les boules fermées de rayon t centrées sur les mots de code doivent être disjointes. La capacité de correction d'un code correspond au plus grand entier t vérifiant cette propriété, c'est aussi le plus grand entier strictement plus petit que δ/2. Elle permet de définir une première majoration, appelée borne de Hamming :
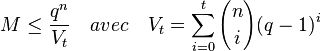
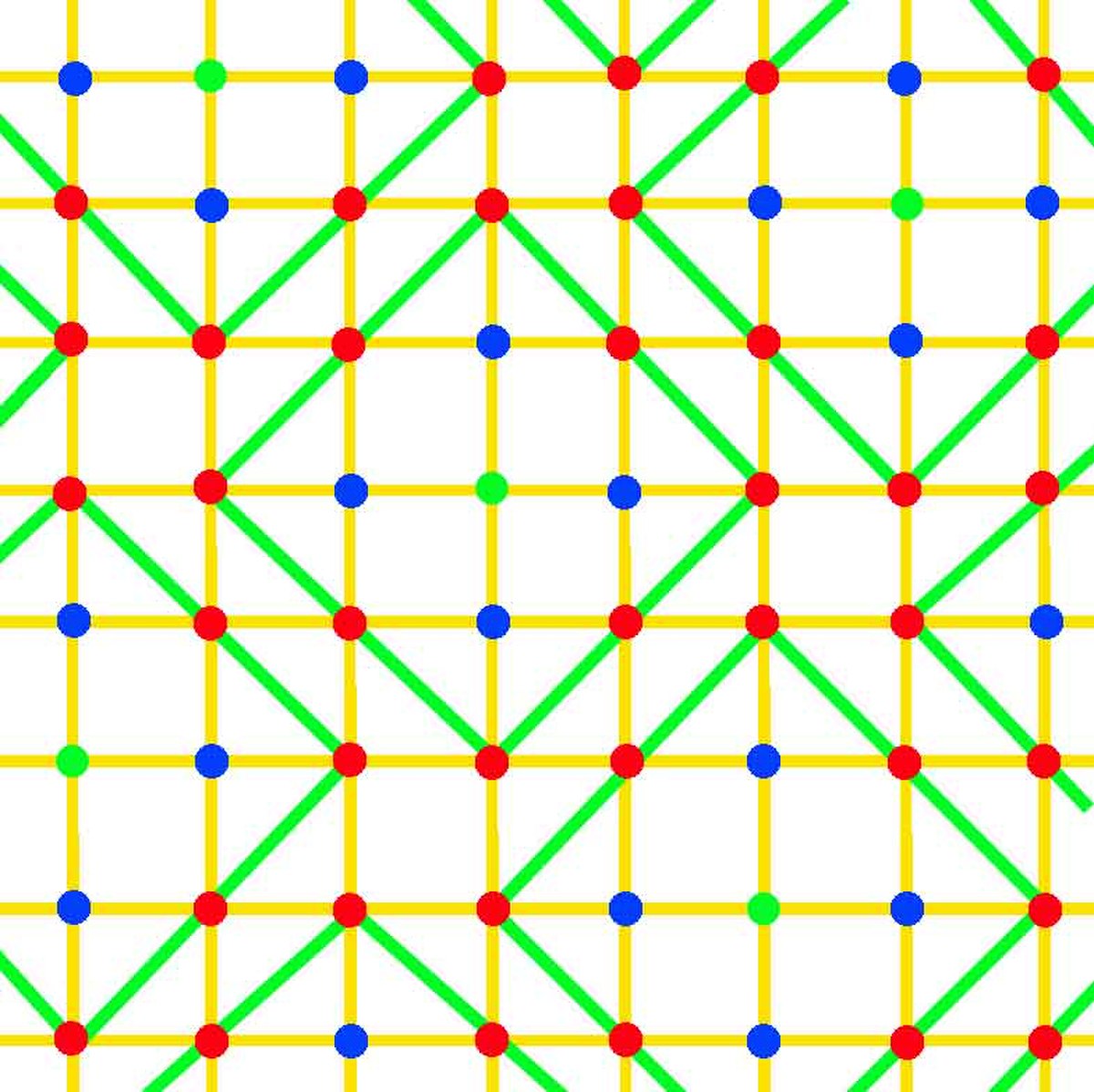
La figure de gauche correspond à une configuration idéale, correspondant au cas où les boules fermées de rayon t et de centre les mots du code forment une partition de l'espace F. Les points du code, en vert, sont espacés d'une distance de cinq entre eux. Si la transmission ne produit jamais plus de deux altérations, alors les erreurs sont toutes corrigibles. Les points à une distance de un d'un mot de code sont en bleu, ceux à une distance de deux en rouge et la frontière des boules est indiquée en vert. Il n'existe aucune redondance inutile, le code est le plus compact possible pour garantir la correction certaine de t erreurs. Pour de tels codes, la majoration de la borne de Hamming est une égalité. Ils sont dit parfaits. L'exemple le plus simple est celui de Hamming binaire de paramètres [7,4,3].
Quelques applications typiques
La transmissions d'informations peut-être sujet à des perturbations. Voici quelques applications touchés par ces perturbations :
- les téléphones cellulaires sont mobiles, relativement peu puissants, et souvent utilisés soit loin des antennes relais, soit dans un environnement urbain très bruyant du point de vue électromagnétique;
- les sondes spatiales n'ont pas à leur disposition d'énormes quantités d'énergie pour émettre des messages, se trouvent à des distances astronomiques, et leur antenne, même si elle est orientée le mieux possible, n'est pas parfaite;
- en cas de conflit armé, les communications adverses sont une des cibles privilégiées pour le brouillage et la guerre électronique
- les images disque contiennent pour certains formats (par exemple Mode 2 Form 1) des codes EDC et ECC pour contrôler les données gravées, et cela par secteur.