Code correcteur - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un code correcteur est une technique de codage basée sur la redondance. Elle est destinée à corriger les erreurs de transmission d'une information (plus souvent appelée message) sur une voie de communication peu fiable.
La théorie des codes correcteurs ne se limite pas qu'aux communications classiques (radio, câble coaxial, fibre optique, etc.) mais également aux supports pour le stockage comme les disques compacts, la mémoire RAM et d'autres applications où l'intégrité des données est importante.
Problématique
Description intuitive
Les codes correcteurs d'erreurs ont leur source dans un problème très concret lié à la transmission de données. Dans la grande majorité des cas, une transmission de données se fait en utilisant une voie de communication, le canal de communication, qui n'est pas entièrement fiable. Autrement dit, les données, lorsqu'elles circulent sur cette voie, sont susceptibles d'être altérées.
Par exemple lors d'une communication radio, la présence de parasites sur la ligne va perturber le son de la voix. Il y a alors essentiellement deux approches possibles :
- augmenter la puissance de l'émission
- ajouter de la redondance à l'information
Si l'on reprend l'exemple de la communication radio, augmenter la puissance de l'émission signifie crier ou avoir un meilleur émetteur. Cette technique a bien évidemment ses limites, et aura du mal à être utilisée dans des sondes spatiales, sans même prendre en considération des contraintes sur les ressources en énergie.
L'autre solution va consister à ajouter des données, ce qui donne lieu au code des aviateurs qui diront «Alpha Tango Charlie» dans le seul but de transmettre correctemment «ATC» à travers leur radio. La séquence «Alpha Tango Charlie», même déformée par la friture, sera bien plus reconnaissable pour l'oreille humaine qu'un «ATC» déformé.
Classification de la problématique

Les problématiques apportées par l'industrie sont diverses. Dans le cas de la transmission de données, par exemple sur internet, le rôle du code correcteur se limite parfois à la détection des erreurs. C'est le cas pour le protocole TCP. La correction est alors réalisée par une nouvelle demande de transmission du message.
Pour d'autres situations, l'objectif est la correction d'erreurs, sans nouvelle demande de transmission. Là encore, plusieurs configurations se présentent. La communication sur ordinateur par le port série utilise un code dont l'objectif est la correction de petites erreurs relativement fréquentes mais isolées. Dans le cas du disque compact, les erreurs sont aussi causées par des rayures ou des impuretés du support, elles sont moins fréquentes mais beaucoup plus volumineuses. La norme de la société Philips impose la capacité de correction d'erreurs dans le cas d'une rayure de 0,2 millimètre, dans la pratique, le code utilisé corrige jusqu'à 4096 bits consécutifs soit une rayure de plus d'un millimètre de large.
Le disque compact présente une nouvelle situation, celle de l' effacement. Dans ce contexte, et à la différence du paragraphe précédent, le message transmis possède l'indication de la détérioration. La détection des erreurs n'est plus nécessaire, toute l'information se concentre sur la reconstitution du message détérioré.
Cette variété de situations explique la multiplicité des techniques utilisées pour les codes correcteurs. On peut citer les sommes de contrôle pour la simple détection, le code BCH pour les ports série ou encore une variante du code de Reed-Solomon pour les disques compacts. Beaucoup de solutions industrielles sont hybrides, comme par exemple le code de Hamming ou encore celui utilisé pour le Minitel.
D'autres contraintes industrielles se greffent sur la problématique des codes correcteurs. Le coût d'implémentation en est un exemple. Pour une solution grand public, la technique d'encodage et de décodage doit être peu onéreuse. La vitesse de reconstitution des messages est aussi un facteur pris en compte.
Redondance et fiabilité
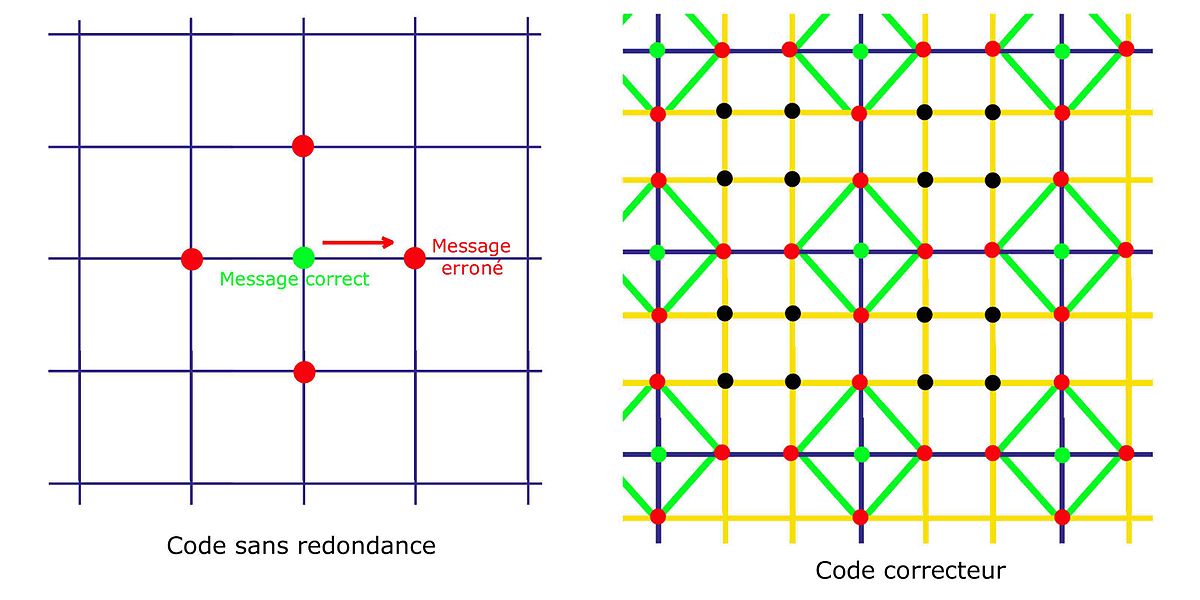
Tous les codes correcteurs subissent une contrainte du même ordre. Si le message contient une information altérée, une information supplémentaire est nécessaire pour, soit détecter l'erreur, soit la corriger. La formalisation est la suivante. Le message transmis, appelé code est plongé dans un espace plus vaste, comme illustré dans la figure de droite.
Le cas d'un code sans redondance est illustré à gauche. Si un message en vert subit, lors de sa transmission, une altération, alors un nouveau message en rouge est transmis. Aucune information ne laisse supposer qu'une erreur a été commise. Pour pallier cet état, l'objectif est d'entourer les messages licites, correspondant aux intersections des quadrillages sur les figures, par des messages connus pour contenir des erreurs, et de réaliser la transmission après. Ces redondances sont illustrées sur la figure de droite par les intersections du quadrillage orange. Si une unique erreur se produit, alors le message transmis correspond à un point rouge. Si la redondance a été habilement construite, alors il n'existe qu'un point licite en vert proche du point rouge reçu.
Un code correcteur propose une géométrie où les messages licites sont le plus possible éloignés les uns des autres. Les boules centrées sur les bons codes, si elles ne s'intersectent pas, permettent de retrouver le bon message, correspondant à son centre. Une perturbation, tant qu'elle reste suffisamment petite pour ne pas faire sortir le code de sa boule est corrigible.
Les points noirs ne sont d'aucune utilité. Il est nécessaire de parcourir deux segments du quadrillage pour relier un point noir d'un point licite. Le code correcteur illustré engendre alors une ambiguïté. En effet, tous les points rouges sont à une distance de deux segments de deux points verts, une double erreur n'est donc généralement pas corrigible. Les points noirs ne servent à rien et ils prennent de la place. Ils présentent une redondance inutile.
Structures mathématiques
Créer une bonne géométrie optimale rapide et peu chère demande de structurer l'espace des codes. Ces structures sont essentiellement réalisées avec des outils mathématiques. L'utilisation des corps finis est presque universelle. L'un est particulièrement utilisé, celui noté F2 correspondant au corps à deux éléments 0 et 1. La théorie des corps finis démarre par les travaux de Frobenius . Il utilise la théorie de Galois pour expliciter leur comportement. Ses travaux sont la base de nombreux développements de la théorie des codes correcteurs. Ces corps sont particulièrement adaptés.
- Ils correspondent à des structures discrètes par opposé à continu. En conséquence ils sont plus simples à modéliser par l'électronique et l'informatique.
- Ils forment la base de nombreux développements. La théorie des espaces vectoriels permet la création de géométrie utile. L'algèbre linéaire est adapté à la mesure du volume des redondances inutiles, ils servent de support à toute une famille de codes correcteurs: les codes linéaires. L'anneau des polynômes à coefficients dans un corps fini est riche en propriétés. Il permet de généraliser la notion de preuve par neuf avec des améliorations notoires (cf l'article Somme de contrôle). Dans ce cas, si la détection d'altérations est possible, la correction automatique ne l'est pas. Les polynômes possèdent des propriétés analogues, et la localisation des erreurs devient possible. De plus, la multiplication est particulièrement aisée. Elle correspond à celle des entiers avec en moins le problème de la retenue. Or, en informatique, la retenue représente l'essentiel du temps de calcul. Beaucoup de codes correcteurs se fondent sur les propriétés des polynômes, ils sont regroupés sous le nom de code cyclique. Enfin, l'arithmétique moderne utilise largement les corps finis, à travers des outils comme les fonctions elliptiques. S'ils demandent un niveau d'abstraction élevé, ils permettent d'obtenir des résultats difficiles. Elles sont utilisées pour certains codes correcteurs, comme celui de Goppa, leur importance industrielle est néanmoins pour l'instant encore faible.