Code correcteur - Définition

Théorie algébrique des codes en blocs

Si l'analyse qu'apporte la distance de Hamming et les codes parfaits propose un cadre permettant d'évaluer l'efficacité d'un code, elle n'offre pas de solution pratique pour en construire.

La solution consiste à équiper les ensembles E et F de structures algébriques plus riches. Pour cela, les alphabets A et A' sont identifiés et munis d'une structure de corps fini. Le cas le plus fréquent consiste à choisir le corps F₂ ou l'une de ses extensions finies. Ce corps correspond à l'alphabet binaire dont les tables d'addition et de multiplication sont données ci-dessous:

Ce corps, ou ses extensions sont adaptés à un traitement informatique, qui, dans sa grande généralité travaille sur l'alphabet binaire.

Codes linéaires

Si les alphabets sont un même corps finis E et F héritent naturellement d'une structure d'espace vectoriel. Choisir alors l'application d'encodage φ une application linéaire simplifie grandement la problématique.

Les paramètres d'un code linéaire sont notés de manière légèrement différente de ceux des codes quelconques. L'espace E est vectoriel, il est décrit uniquement par sa dimension, correspondant à la longueur du code. Ils sont notés [n,k, δ].

Peu de codes linéaires sont parfaits, et ils sont soit de petites dimensions soit de petite distance minimale. Une autre majoration, plus générale et de même nature que la borne de Hamming existe :

• La majoration suivante est vérifiée pour tous les codes linéaires. Elle se nomme borne de Singleton :

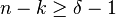
Si la borne est atteinte, on parle alors de code MDS pour maximum distance séparable.

Matrice génératrice

L'encodage est obtenu par l'application d'une matrice, dite matrice génératrice. Elle est toujours équivalente à une forme particulièrement simple, appelée code systématique, les premières coordonnées d'un mot du code correspondent au message, les dernières décrivent la redondance, elles sont appelées sommes de contrôle ou, dans le cas d'un code cyclique contrôles de redondance cyclique.

Matrice de contrôle

La validation du décodage est encore simplifiée. Il existe une application linéaire de F dans un espace de dimension n -k ayant comme noyau exactement le code. Sa matrice est dite de matrice de contrôle. Dans le cas, le plus fréquent dans l'industrie, du code systématique, la matrice de contrôle s'obtient directement à partir de la matrice génératrice et elle possède encore une forme particulièrement simple.

Valider un message reçu revient à vérifier que l'application de la matrice de contrôle à ce message est bien égale au vecteur nul.

Syndrome et décodage

La linéarité du code assure un décodage aisé. Si un message x est reçu, alors la détection d'erreurs est réalisée par la matrice de contrôle H. En effet, des altérations détectables ont eu lieu si et seulement si H.^tx est différent du vecteur nul. Si le nombre d'erreurs présentes dans le message est inférieur à t, le nombre d'altérations assurément détectables, alors H.^tx possède un unique antécédent e dans la boule fermée de centre le vecteur nul et de rayon t. Le message corrigé est x - e. Le vecteur H.^tx est appelé syndrome.

Dans le cas où le nombre d'erreurs est supérieur à t il existe plusieurs antécédents de poids minimal et les altérations ne sont plus assurément corrigibles. La solution idéale consiste à demander une nouvelle transmission.

Si le nombre de syndromes est petit, une table de correspondance entre les syndromes et leurs antécédents de plus petits poids est envisageable. Une telle table est nommé tableau standard et le décodage associé décodage par tableau standard. Si l'espace des syndromes est trop vaste, il est nécessaire de calculer son antécédent à la réception du message altéré.

Codes cycliques

Ces codes sont plus compliqués et reposent sur l'utilisation des propriétés des polynômes dans un corps fini. Le contrôle de redondance cyclique (CRC pour cyclic redundancy check) consiste à considérer un bloc de données comme la représentation des coefficients d'un polynôme que l'on divise ensuite par un polynôme fixe et prédéterminé. Les coefficients issus de cette division constituent le CRC et servent de code correcteur. La vérification des données se fait en multipliant le polynôme fixe par les coefficients du CRC et en comparant le résultat avec les données. On peut également calculer le CRC des données reçues et comparer avec le CRC reçu.

Autres codes

Les structures utilisées dans les codes correcteurs ont tout d'abord été très simples (par exemple celle d'espace vectoriel), puis se sont complexifiés avec une meilleure compréhension des problèmes théoriques. La théorie des codes correcteurs en arrive même à utiliser la géométrie arithmétique pour construire des codes.