Corps de décomposition - Définition

Exemples

Le corps de décomposition du polynôme X²+1 sur le corps des nombres réels est le corps des nombres complexes.

Construisons alors le corps de décomposition L du polynôme P(X) = X³ - 2 sur le corps des nombres rationnels. Soit r la racine cubique (réelle) de 2, et j la racine cubique (complexe) de l'unité ayant une composante imaginaire positive. Alors les deux autres racines sont j.r et j².r. Aucune racine n'est rationnelle, donc le polynôme est irréductible (en effet tout polynôme de degré trois qui n'est pas irréductible possède une racine rationnelle).

Considérons l'extension K₁ égale à Q(r), c’est-à-dire l'extension engendrée par r. Comme P(X) est irréductible, c'est une extension de degré trois isomorphe à Q[X]/(P(X)Q[X]) (cf le paragraphe Extension algébrique et polynôme) et dont une base est {1, r, r²}.

Sur K₁ le polynôme P(X) possède une racine r. Une division de P(X) par le polynôme X - r donne l'égalité:

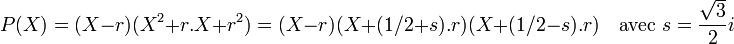
On en déduit que L est égal à K₁(s) qui est une extension de degré deux de K₁ et dont une base est {1, s}.

On a l'égalité sur les degrés [L:Q] =[L:K₁].[K₁:Q]= 3 x 2 = 6 (cf. Définitions et premières propriétés des extensions algèbriques). On en déduit une base de L sur K qui est {1, r, r²,s ,s.r, s.r²}.

Remarque: la méthode présentée ici est générique, elle peut être utilisée pour bâtir des corps de décomposition.