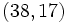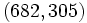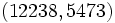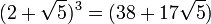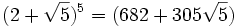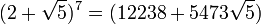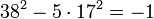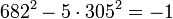Équation de Pell-Fermat - Définition
La liste des auteurs de cet article est disponible ici.
Équation de Pell et entier algébrique
Si (a, b) satisfait une équation de Pell du type x2 -n.y2 = ±1, alors a + √n.b est un élément du groupe des unités de l'anneau des entiers de l'extension algébrique Q[√n]. Un élément du groupe des unités est un élément inversible dans l'anneau, l'égalité (a + √n.b).(a - √n.b) = ±1 montre de fait que l'élément est inversible.
Le groupe des unités ainsi que l'équation de Pell est étudié dans le cas où le paramètre est égal à cinq dans l'article Entier de Dirichlet, cette analyse montre la relation entre les équations de Pell et la théorie algébrique des nombres. L'analyse de cet anneau d'entiers a permis à Dirichlet et Legendre de trouver la démonstration du dernier théorème de Fermat dans le cas où le paramètre est égal à cinq.
Cas x²-ny² = -1
On démontre que si
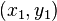
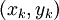
-
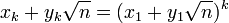
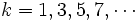
sont les solutions générales.
Exemple
Une solution particulière de
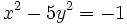
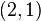
Les développements :
fournissent les solutions