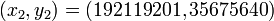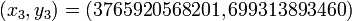Équation de Pell-Fermat - Définition
La liste des auteurs de cet article est disponible ici.
Définitions
Une équation diophantienne est une équation dont les solutions recherchées sont en général entières et parfois rationnelles. Ici, ce sont les solutions entières qui sont étudiées. Un autre terme est utilisé dans la définition :
-
- Un entier strictement supérieur à 1 est dit sans facteur carré si et seulement s'il n'existe aucun carré parfait autre que un le divisant.
La définition de l'équation est la suivante :
-
- Une équation de Pell-Fermat est une équation diophantienne de la forme suivante, si n est un entier strictement positif non carré parfait et m un entier non nul quelconque :
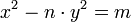
Pour trouver toutes les solutions, si elles existent, il est nécessaire d'analyser le cas où m est inversible, c'est-à-dire s'il est égal en valeur absolue à un. Ce cas est suffisamment important pour que parfois l'équation de Pell-Fermat ne désigne que le cas où m est égal à 1, ou ±1. Il est commode de travailler dans le corps des nombres de la forme α + √n.β, ici α et β désignent deux rationnels. Cette double raison est la motivation des deux définitions suivantes :
-
- Une racine ou unité de l'équation est un nombre réel ρ de la forme a + √n.b, avec a et b deux entiers, tel que ρ.ρ' soit égal à ±1, ici ρ' désigne le nombre a - √n.b, appelé conjugué de ρ.
Un intérêt de la définition précédente provient du fait que les coefficients de r vérifient l'égalité suivante et que tout couple d'entiers satisfaisant cette égalité définit une racine.
-
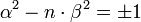
- Une solution ω est dite primitive ou unité fondamentale si et seulement si, pour toute solution ρ il existe un entier e égal à 1 ou -1 et un entier relatif k tel que ρ soit égal à e.ω k.
Cas x²-ny² = 1
On démontre alors :
- Si
![\sqrt n = [a_0, \overline{a_1,a_2,a_3,\ldots,a_{m-1},a_m}]](https://static.techno-science.net/illustration/Definitions/autres/e/ecc46808ab8565a77fba83681cc57a5c_39c820ae93447d31f116ac6dfe419330.png)
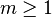
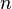
- l'équation de Pell
![\sqrt n = [a_0, \overline{a_1,a_2,a_3,\ldots,a_{m-1},a_m}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/ecc46808ab8565a77fba83681cc57a5c_39c820ae93447d31f116ac6dfe419330.png)
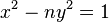
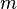
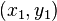
- quand
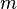
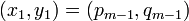
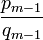
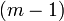
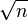
- quand
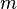
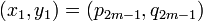
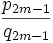
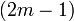
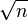
- La réduite de rang
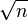
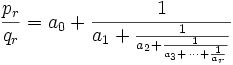
- Les autres solutions
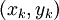
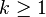
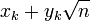
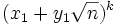
- En particulier,
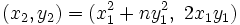
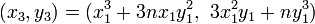
- La formule de récurrence étant :
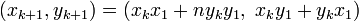
Exemples détaillés
- Recherche des solutions de
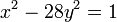
- Le développement en fraction continue périodique de
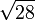
![[5, \overline{3,2,3,10}]](https://static.techno-science.net/illustration/Definitions/autres/7/735283530cf3311d3e7c70c12db613ce_7c621f717f20f239940a24ae275f3c4e.png)
- La réduite de rang (m − 1) = 3 de
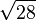
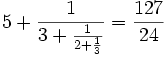
- La solution minimale est donc
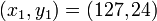
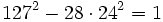
- Les autres solutions sont
![[5, \overline{3,2,3,10}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/735283530cf3311d3e7c70c12db613ce_7c621f717f20f239940a24ae275f3c4e.png)
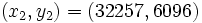
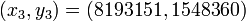
- Recherche des solutions de
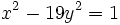
- Le développement en fraction continue périodique de
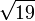
![[4, \overline{2,1,3,1,2,8}]](https://static.techno-science.net/illustration/Definitions/autres/e/e004a43067c406e2c1eb4c298d3d42a4_33ffb0f52cb6ece8eacf999d46679757.png)
- La réduite de rang (m − 1) = 5 de
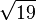
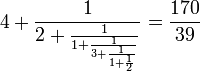
- La solution minimale est donc
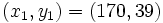
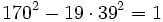
- Les autres solutions sont
![[4, \overline{2,1,3,1,2,8}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e004a43067c406e2c1eb4c298d3d42a4_33ffb0f52cb6ece8eacf999d46679757.png)
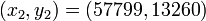
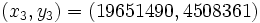
- Recherche des solutions de
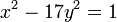
- Le développement en fraction continue périodique de
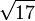
![[4, \overline{8}]](https://static.techno-science.net/illustration/Definitions/autres/6/67b838bcf2f5e3c55042d35d96ad8606_e6855b8de040a6d919386248324b7e09.png)
- La réduite de rang (2m − 1) = 1 de
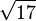
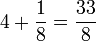
- La solution minimale est donc
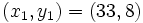
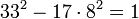
- Les autres solutions sont
![[4, \overline{8}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/67b838bcf2f5e3c55042d35d96ad8606_e6855b8de040a6d919386248324b7e09.png)
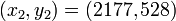
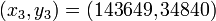
- Recherche des solutions de
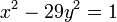
- Le développement en fraction continue périodique de
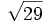
![[5, \overline{2,1,1,2,10}]](https://static.techno-science.net/illustration/Definitions/autres/5/53047c853c44836ae8af265787d0aa1b_f03425538c3ae3220172fea86e716ade.png)
- La réduite de rang (2m − 1) = 9 de
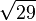
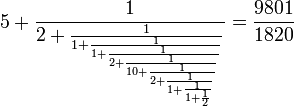
- La solution minimale est donc
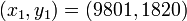
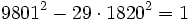
- Les autres solutions sont
![[5, \overline{2,1,1,2,10}]](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/53047c853c44836ae8af265787d0aa1b_f03425538c3ae3220172fea86e716ade.png)
