Équation de Pell-Fermat - Définition

Introduction

Pierre de Fermat montre que l'équation de Pell-Fermat possède toujours une infinité de solutions si m est égal à un en valeur absolue.

En mathématiques et plus précisément en arithmétique, l'équation de Pell-Fermat est une équation diophantienne polynomiale quadratique. Si n est un entier strictement positif, non carré parfait et m un entier quelconque, l'équation prend la forme suivante :

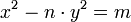
Les solutions recherchées sont les solutions telles que x et y soient des valeurs entières.

L'équation de Pell-Fermat est étudiée sous différentes formes par plusieurs civilisations comme la Grèce antique, l'Inde ou la civilisation arabe. La solution définitive est relativement tardive, elle est trouvée en Europe durant le XIX^e siècle.

Une forme particulièrement étudiée est celle où le paramètre m est égal à plus ou moins un. Plusieurs algorithmes permettent de déterminer une solution, la méthode chakravala ou celle des fractions continues sont les plus célèbres. L'étude des entiers quadratiques, un outil issu de la théorie algébrique des nombres, est nécessaire pour démontrer l'exhaustivité de la solution.

En France, cette équation est nommée Pell ou Pell-Fermat en l'honneur des mathématiciens, John Pell et Pierre de Fermat . C'est à Leonhard Euler que l'on doit l'association du nom de Pell à cette équation, à la suite d'une confusion car ce mathématicien n'a pas travaillé sur cette équation. La traduction de la dénomination équation de Pell est d'usage général en langue non française.

L'article Fraction continue d'un nombre quadratique propose une méthode de résolution si m est égal à ±1, ainsi que l'exemple pour la valeur de n égale à 61. L'article Méthode chakravala propose une autre méthode comparable, plutôt plus simple et plus rapide, à la fois pour la théorie et la pratique. Les exemples pour les valeurs de n suivantes : 19, 61, 83, 103 et 313 sont traités.

Histoire

Origines

L'histoire de l'équation de Pell-Fermat est particulièrement riche et ancienne. On cite parfois le problème des bœufs d'Hélios posé par Archimède comme premier exemple d'équation de Pell-Fermat. Il n'est cependant pas certain qu'Archimède en soit l'auteur et que la relation avec la dite équation ait été faite. En revanche, Diophante d'Alexandrie, un mathématicien vivant probablement au III^e siècle parle explicitement d'une équation de cette nature, dans son livre intitulé Arithmetica. Avec les notations du paragraphe Définitions, il étudie le cas où n est égal à 1 et m à 1, -1 ou 12 ainsi que le cas ou n et m sont égaux à 9. Dès avant notre ère, les grecs connaissaient l'existence de l'égalité suivante :

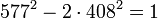
Le mathématicien indien Brahmagupta semble être le premier à travailler profondément sur la question, il étudie le cas où m égal à un. En 628, il établit une égalité permettant, à l'aide de deux solutions de l'équation, d'en construire une troisième. Ainsi, en combinant deux fois la même solution, il en obtient une nouvelle et ainsi de suite, ce qui donne un nombre de solutions aussi grand que désiré. Cette méthode lui permet d'aller plus loin. A l'aide d'un couple (x, y) d'entiers tel que x² - n.y² soit égal à 2 en valeur absolue, Brahmagupta construit une solution. Puis à l'aide d'un algorithme guère plus complexe, il obtient un résultat analogue si x² - n.y² est égal à 4 en valeur absolue. Par tâtonnements, il parvient à trouver des solutions dans de nombreuses configurations. Son outil principal est l'algorithme d'Euclide, généralement nommé par les indiens le pulvérisateur car il casse les nombres en morceaux de plus en plus petits.

L'étape suivante est franchie par Bhāskara II un mathématicien indien vivant au XII^e siècle. Il enrichit la palette de techniques de Brahmagupta, et présente une méthode complète, nommée chakravala. Elle correspond à un algorithme astucieux permettant de déterminer une solution primitive, c'est-à-dire une solution qui génère toutes les autres. Il n'est pas dans l'usage des mathématiciens indiens de cette époque de rechercher une preuve autre qu'expérimentale. Quant à l'exhaustivité de l'ensemble des solutions trouvées, la question n'est pas non plus abordée.

L'Europe et l'âge classique

Joseph-Louis Lagrange démontre l'existence d'une infinité de solutions si m est égal à ±1 et montre que l'algorithme des fractions continues permet de les obtenir toutes.

La popularité de cette équation provient d'un défi que Pierre de Fermat lance aux mathématiciens de l'Europe entière. Le 3 janvier 1657, il pose plusieurs questions dont celle d'une solution à l'équation de Pell-Fermat, déjà trouvée par Brahmagupta et Bhāskara II, elle correspond au cas n = 61 et m = 1. Il termine sa lettre par « J'attends la solution de ces questions ; si elle n'est fournie ni par l'Angleterre, ni par la Gaule Belgique ou Celtique, elle le sera par la Narbonnaise ». Les mathématiciens visés sont Kenelm Digby, William Brouncker et John Wallis pour l'Angleterre, Frans van Schooten pour la Gaule Belgique et Bernard Frénicle de Bessy pour la Gaule Celtique. Une communication épistolaire s'ensuit, finalement publiée par Wallis. Elle nous indique que Brouncker découvre une méthode équivalente à celle des Indiens, sans néanmoins apporter plus de preuves que ses prédécesseurs. Frénicle de Bessy calcule l'intégralité des solutions pour n inférieur ou égal à 150, mais ses travaux sont perdus. Il défie Brouncker avec une valeur de 313 pour n. Brouncker propose une solution primitive, et précise qu'il ne lui a pas fallu plus d'une heure ou deux pour trouver. La réponse est la suivante :

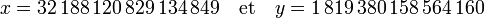
Wallis démontre rigoureusement les découvertes de Brahmagupta, c'est-à-dire la raison qui permet de trouver une solution si la valeur atteinte est 2 ou 4 en valeur absolue. En 1658, Johann Heinrich Rahn publie un livre d'algèbre, contenant un exemple d'équation maintenant dite de Pell-Fermat, relu et traduit en anglais par John Pell. C'est la seule contribution connue du mathématicien sur l'équation portant maintenant son nom.

Plusieurs mathématiciens affirment qu'il existe une solution pour toute valeur de n (à condition de choisir m égal à 1), Fermat affirme de plus que le nombre de solutions est infini. En revanche aucune preuve de cette époque n'est connue.

Leonhard Euler reprend les travaux de Brouncker et ceux de Wallis, proposant le formalisme de la fraction continue, équivalent à l'algorithme développé par Bhāskara II. Seule la fin est différente, une fois trouvée une valeur égale à 2 ou 4 en valeur absolue, il est en effet plus rapide d'utiliser le lemme de Brahmagupta. Euler attribue à tort les travaux passés à Pell. Joseph-Louis Lagrange reprend les travaux d'Euler et ajoute les deux preuves manquantes. Il démontre que pour toute valeur de n il existe une infinité de solutions et que toutes ces solutions sont générées par celle issue de l'algorithme des fractions continues. Durant toute cette époque, l'Europe est inconsciente des travaux de leurs prédécesseurs indiens.

XIX^e siècle

Richard Dedekind formalise le concept d'anneau portant maintenant son nom et élucide les propriétés permettant de résoudre l'équation de Pell-Fermat.

La méthode Chakravala ou celle des fractions continues ont apporté tout ce qu'elles pouvaient sur cette équation, ce qui revient à traiter le cas du paramètre m égal à ±1. Le cas général demande de nouvelles idées et un siècle est encore nécessaire pour en venir à bout. Une approche fondatrice est l'œuvre de Carl Friedrich Gauss . Il travaille sur des structures munies d'une addition et d'une multiplication, mais qui ne sont pas celles de l'anneau des entiers. Une de ces structure est celle des entiers de Gauss, c'est-à-dire des nombres de la forme a + i.b où a et b sont des entiers et i l'unité imaginaire des nombres complexes. Un tel monde possède une division euclidienne, ce qui permet d'établir le théorème de Bachet-Bézout, le lemme d'Euclide ainsi que le théorème fondamental de l'arithmétique. Un tel anneau possède des nombres premiers de Gauss, et une approche similaire à celle de l'arithmétique dans Z est possible. Cette approche est maintenant le cadre d'une théorie appelée arithmétique modulaire. Une démarche de cette nature permet de venir à bout d'une équation diophantienne semblable à celle de Pell-Fermat, traité par le théorème des deux carrés de Fermat. Si i est remplacé, par exemple par le nombre d'or, égal à 1/2(1 + √5) on obtient une structure un peu similaire, aussi euclidienne, correspondant à l'équation de Pell-Fermat pour le paramètre n égal à 5, et il est possible d'y traiter l'équation pour toute valeur du paramètre n (cf Anneau des entiers de Q(√5)), à condition de disposer de la loi de réciprocité quadratique, démontrée par Gauss. Cette loi correspond encore à une équation diophantienne un peu similaire.

Les travaux de Gauss apportent deux progrès : ils offrent un bon cadre pour étudier l'équation de Pell-Fermat et ils permettent de la résoudre intégralement dans le cas où ce cadre est euclidien. Il existe cependant de nombreux cas où le caractère euclidien est absent. Ce cadre, euclidien ou non, porte le nom d'anneau d'entiers algébriques et pour la résolution de l'équation de Pell-Fermat, une petite partie est utile, ceux formés par des entiers quadratiques. Johann Peter Gustav Lejeune Dirichlet étudie et explicite leur groupe des unités dans le cas général. Ce groupe correspond exactement aux solutions l'équation de Pell-Fermat pour m = ±1, fournissant une preuve différente de celle de Lagrange, et qui se généralise à tous les anneaux d'entiers algébriques et non pas uniquement quadratiques. Si ce résultat fait progresser la théorie des nombres, il ne permet pas de débloquer la question de l'équation de Pell-Fermat dans le cas général, car il ne concerne que les solutions pour le paramètre m = ±1.

Si les techniques de Gauss fonctionnent, c'est grâce à l'équivalent des nombres premiers et au théorème fondamental de l'arithmétique, que l'on trouve dans tout anneau euclidien. Des anneaux disposant de propriétés ou d'axiomes plus faibles ont un équivalent, on les appelle les anneaux factoriels. Dans le cas général, un anneau d'entiers algébriques n'est ni euclidien ni factoriel. Richard Dedekind , à la suite des travaux de Ernst Kummer , trouve la bonne approche. Il met en évidence les axiomes que vérifient les bons anneaux d'entiers algébriques, ils portent maintenant le nom d'anneau de Dedekind. À l'aide de cette nouvelle structure, il établit un équivalent du théorème fondamental de l'arithmétique. Un deuxième théorème, traitant du groupe des classes d'idéaux permet de trouver toutes les solutions de l'équation de Pell-Fermat et pour toutes valeurs de n.