Équation de Pell-Fermat - Définition

Cas où m est égal à ±1

Dans toute la suite de l'article, les lettres Z, Q et R désignent respectivement les entiers relatifs, les nombres rationnels et les nombres réels.

Une première étude consiste à résoudre le cas où m est égal à ±1. Elle peut être vue soit comme une finalité, soit comme une étape nécessaire à la résolution complète de l'équation. Souvent le terme d'équation de Pell-Fermat ne désigne que ce cas particulier.

Il existe trois approches théoriques différentes dont deux proposent une méthode effective pour la résolution. La première méthode, au sens de l'histoire, est la plus efficace en terme algorithmique, c'est aussi plutôt la plus simple pour une approche théorique, elle porte le nom de chakravala donné par ses inventeurs indiens. La deuxième se fonde sur les fractions continues. Historiquement, elle est à la source de la première démonstration théorique connue de la structure des solutions. La troisième, issue de la théorie algébrique des nombres est la plus puissante, elle procède d'une démarche à même de résoudre intégralement l'équation.

Méthode chakravala

Cette méthode part initialement d'une utilisation judicieuse de la formule suivante, nommée identité de Brahmagupta :

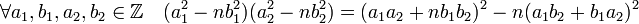
Ainsi, si (a₁, b₁) et (a₂, b₂) forment deux couples de solutions, l'identité précédente montre que (a₁.a₂ + n.b₁.b₂, a₁b2 + a₂b1) est encore une solution. Si l'on note G l'ensemble des solutions de l'équation il est judicieux d'équiper l'ensemble d'une loi de composition interne * :

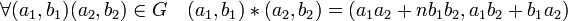
La loi * est une loi de composition interne d'après l'identité de Brahmagupta, le couple (1,0) est l'élément neutre, elle est associative, chaque élément (a₁, b₁) possède un symétrique (a₁, -b₁), enfin la loi est commutative. Ainsi (G, *) forme un groupe abélien.

L'étude de ce groupe permet la mise au point d'une méthode efficace de résolution pour les valeurs de m égales à 1 ou -1. Par exemple, si α est un élément de G, solution pour la valeur m = -1, α² est une solution pour la valeur m = 1. Si α est solution pour la valeur m = +/-2 alors 1/2.α² est une solution pour la valeur m = 1. Enfin, si α est solution pour la valeur m = +/-4 alors 1/8.α³ est une solution pour la valeur m = +/-1.

L'article détaillé propose une méthode exhaustive permettant de trouver une solution dans tous les cas, à partir des propriétés de la multiplication *. Il montre aussi comment cette méthode permet d'élucider la structure du groupe des solutions.

Une manière commode de voir ce groupe est d'identifier le couple (a₁, b₁) avec le nombre réel a₁ + √n. b₁. Cet ensemble forme un anneau, noté A dans cet article. Le groupe G s'identifie au groupe des unités de A, c'est-à-dire au groupe des éléments inversibles de l'anneau, muni de la multiplication des nombres réels. Pour cette raison, une solution de l'équation s'écrit souvent a₁ + √n. b₁. Une identité remarquable montre la relation :

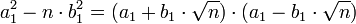
Groupe des unités

Résoudre l'équation (1) revient finalement à expliciter les éléments du groupe des unités de l'anneau A, c'est-à-dire l'ensemble des éléments ayant un inverse. Ce groupe est isomorphe au produit direct du groupe cyclique à deux éléments Z/2Zet de Z. Il existe toujours un élément α du groupe qui engendre toutes les autres, ce qui justifie la définition d'unité fondamentale du groupe G, c'est-à-dire un élément α de G tel que :

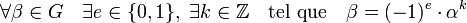
L'existence d'une unité fondamentale pour toute valeur de n strictement supérieur à 1 et sans facteur carré est démontrée dans l'article détaillé. On parle parfois aussi de racine primitive.

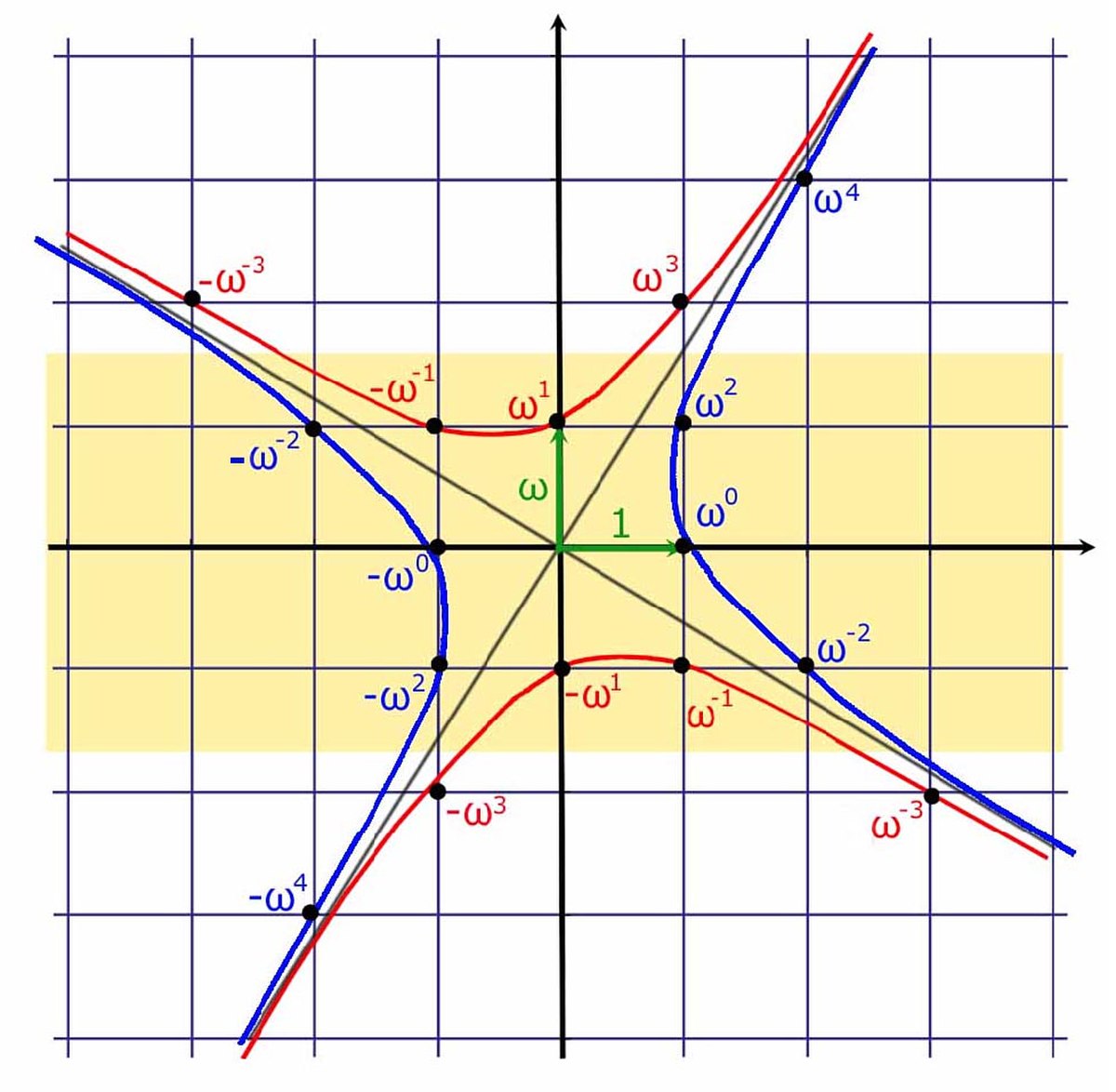
• Soit α une unité fondamentale et a et b deux éléments de Z tel que : α = a + √n. b. Le groupe G contient exactement quatre unités fondamentales : a + √n. b, a - √n. b, -a + √n. b et -a - √n. b.

Cette propriété est une conséquence directe du théorème de structure énoncé en début de paragraphe. La figure de droite illustre le cas où n est égal à 5. La structure de l'anneau est étudiée dans l'article Entier du corps quadratique Q(√5). Les différents éléments de G se trouvent toutes sur quatre branches d'hyperboles. Il existe deux droites asymptotiques d'équation x = +/- √n.y.

Fraction continue

Une solution de l'équation de Pell-Fermat est une bonne approximation fractionnaire de la racine carrée. Dans le cas général, une fraction de type p / q approxime un irrationnel avec une précision de 1/q ou 1/2q. Une solution de l'équation de Pell-Fermat est plus précise. En effet, si (a, b) est une solution :

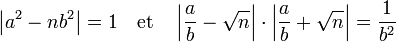
Comme la racine de n ainsi que a / b sont tous les deux strictement supérieurs à 1, on obtient l'approximation suivante :

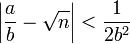
On démontre que les approximations de cette nature sont nécessairement des fractions continues. Ainsi, toute solution (a, b) est composée d'un numérateur et d'un dénominateur d'une réduite d'indice k d'une fraction continue, c'est-à-dire d'une expression de la forme :

Le développement en fraction continue d'un entier sans facteur carré est périodique à partir du deuxième rang, c'est-à-dire qu'il est de la forme suivante, ce qui justifie la notation utilisée :

La période forme un palindrome, selon que la période est paire ou impaire, l'une des deux configurations se produit :

Avec les notations de la ligne précédente, la fraction réduite, solution de l'équation de Pell, si la période est paire est d'indice 2l - 1, si la période est impaire, l'indice est 2l. Par exemple, si n est égal à 29, on trouve f₀ = 5, ce qui correspond à la partie entière de la racine carrée, puis la période [2, 1, 1, 2, 10]. La solution correspond à la fraction continue a/b suivante :

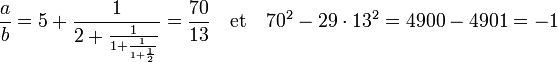
Cette approche permet de démontrer simplement un résultat structurel :

• Il existe une solution u de l'équation (1) telle que pour toute solution s de (1), il existe un entier ε égal à +/-1 et un entier n tel que s = ε.uⁿ.

Autrement dit, il existe une unité fondamentale.

Théorème des unités de Dirichlet