Entier de Dirichlet - Définition

Introduction

Dirichlet

En mathématiques, et plus précisément en arithmétique modulaire, un entier de Dirichlet est un nombre réel de la forme a + b.ω, ici ω désigne le nombre d'or , et a, b deux entiers relatifs. Sur les nombres de cette nature, il est possible de définir une nouvelle arithmétique. Elle est un peu analogue à celle, plus usuelle, des nombres entiers, décrite dans l'article arithmétique élémentaire. Cette arithmétique est à l'origine de bien des propriétés mathématiques du nombre d'or.

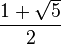
Les entiers de Dirichlet forment un ensemble stable pour l'addition, la soustraction et la multiplication. Il correspond au plus petit ensemble de nombres réels contenant à la fois un et le nombre d'or et stable pour les opérations citées. Sur cet ensemble, il est possible de définir une division euclidienne. On retrouve le lemme d'Euclide, l'identité de Bézout ainsi que le théorème fondamental de l'arithmétique garantissant, en un certain sens l'existence et l'unicité de la décomposition en facteurs premiers d'un entier de Dirichlet. On retrouve les propriétés du plus grand commun diviseur et du plus petit commun multiple et, avec un peu de travail, un équivalent du petit théorème de Fermat. L'analogie ne peut être poussée trop loin, les éléments inversibles pour la multiplication (appelés unités) ne sont pas de même nature dans les deux mondes. À la différence du cas usuel, il n'existe pas deux, mais une infinité de nombres de cette sorte dans l'arithmétique de Dirichlet.

Les entiers de Dirichlet sont utilisés en théorie algébrique des nombres et en arithmétique modulaire, par exemple pour l'étude d'équations diophantiennes. Ces équations sont à coefficients dans les entiers relatifs et les solutions recherchées sont entières. Leur utilisation a permis à Dirichlet et Legendre de démontrer le dernier théorème de Fermat dans le cas où le paramètre est égal à cinq. Les entiers de Dirichlet permettent aussi de résoudre l'équation de Pell-Fermat, encore pour le paramètre cinq.

La relative simplicité de cet univers permet d'élucider sa structure à l'aide des outils de l'arithmétique élémentaire. Ici seuls les théorèmes comme le lemme d'Euclide, l'identité de Bézout ou le petit théorème de Fermat sont utilisés. L'appel à des théories plus puissantes, comme des groupes, des anneaux ou des corps finis permet d'aller plus loin. Il devient possible de comprendre des mondes plus vastes, comme ceux des entiers quadratiques. L'ajout d'autres théories comme la théorie de Galois ou celle des Anneaux de Dedekind permet d'appréhender l'entier algébrique dans sa généralité.

Remarque : Si le contenu mathématique de l'article fait partie du corpus usuel de la théorie des nombres, le terme entier de Dirichlet n'est pas commun. L'ensemble des entiers de cette nature est généralement noté O_Q[√5], il est fréquent de ne pas donner de nom aux éléments.

Éléments d'Histoire

Origines

Leonhard Euler utilise, sans succès une idée précurseur, à l'origine de l'intérêt des entiers de Dirichlet.

L'intérêt pour les propriétés arithmétiques de valeurs analogues au nombre d'or est ancienne. Les indiens de la période classiques développent des outils comme la fraction continue, ou des méthodes pour l'étude d'équations diophantiennes, c'est-à-dire d'équations à coefficients entiers et dont les solutions recherchées sont entières. Brahmagupta , un des mathématiciens à l'origine du zéro, étudie le cas suivant :

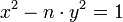
À l'aide d'une identité portant maintenant son nom, il découvre une multiplication entre deux couples de solutions qui donne une troisième solution. Cette méthode, consistant à définir une multiplication sur les couples d'entiers est une des bases de l'arithmétique de Dirichlet.

Plus d'un millénaire plus tard, Leonhard Euler utilise une technique analogue pour une démonstration du dernier théorème de Fermat pour la valeur du paramètre égale à trois. Elle s'avère presque exacte. À deux couples d'entiers, il associe la multiplication * définie par :

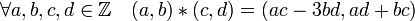
Si cette idée est exactement la même que celle de Brahmagupta, Euler va plus loin. Il remarque que cet ensemble se comporte exactement comme celui des nombres de la forme a + i√3.b, ici i désigne l'unité imaginaire. Ceci garantit plusieurs propriétés comme le fait qu'il existe un élément neutre pour la multiplication : un, que cette multiplication est associative, commutative, distributive par rapport à l'addition et que l'ensemble est intègre, c'est-à-dire que si un produit est nul, alors l'un des facteurs du produit est aussi nul. Cet ensemble comporte finalement les mêmes propriétés ainsi que la même limitation que celui des entiers relatifs, à savoir que de nombreux éléments n'ont pas d'inverse pour la multiplication. Cette analogie pousse Euler à appliquer le théorème fondamental de l'arithmétique dans cet univers, c'est-à-dire à utiliser l'existence et l'unicité d'une décomposition d'un entier de cette nature en nombres premiers pour cet univers. Un nombre premier devient ici un nombre qui, s'il est le produit a.b de deux autres nombres, alors soit a soit b est un élément inversible pour la multiplication. Seul 1 est -1 sont inversibles, dans le monde des entiers relatifs. Euler pousse ici l'analogie trop loin, dans ce monde, 2, 1 + i√3 et 1 - i√3 seraient des nombres premiers, mais :

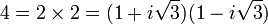
Le théorème fondamental de l'arithmétique ne s'applique pas car il existe plusieurs décompositions en facteurs premiers. L'idée est néanmoins promise à un bel avenir.

Disquisitiones Arithmeticae

Disquisitiones Arithmeticae est le livre de Gauss 1801 formalisant les outils à l'origine de l'intérêt de la démarche de Dirichlet.

En 1801 Carl Friedrich Gauss publie le traité Disquisitiones Arithmeticae, ouvrant la voie à l'arithmétique moderne et aux idées à l'origine de la richesse de l'arithmétique des entiers de Dirichlet. Un seul outil est manquant dans l'univers d'Euler. Si un monde de cette nature dispose d'une division euclidienne, la démarche est parfaitement pertinente. L'identité de Bézout, le lemme d'Euclide, parfois renommé en lemme de Gauss et le théorème fondamental de l'arithmétique s'applique. Gauss utilise cette approche pour formaliser une nouvelle structure, il considère les restes de la division euclidienne par un élément de l'anneau, ces restes sont appelés modulo. Il montre que cet ensemble dispose aussi d'une addition et d'une multiplication. Cette méthode, d'abord développée sur les entiers relatifs est valide sur tous les anneaux euclidiens. Un anneau est un ensemble équipé de deux lois de composition, l'addition et la multiplication. Ces deux lois vérifient toutes les bonnes propriétés pour autoriser les calculs usuels. Gauss applique ces idées aux nombres de la forme a + i.b, qui forment un anneau euclidien. Un tel nombre est maintenant appelé entier de Gauss.

Ferdinand Eisenstein découvre comment contourner la difficulté d'Euler, l'anneau des nombres de la forme a + 1/2(1 + i√3).b est lui euclidien, la démarche d'Euler offre enfin une démonstration rigoureuse pour le grand théorème de Fermat dans le cas du paramètre égal à 3.

Le travail de Dirichlet

La démonstration du cas où le paramètre est égal à 5 s'avère délicate, l'anneau des nombres de la forme a + i√5.b n'est pas euclidien et l'idée d'Eisenstein ne permet pas de venir à bout de cette difficulté. Si le dernier théorème de Fermat devient de plus en plus célèbre, les idées pertinentes tardent à venir. Sophie Germain trouve un premier résultat pour le cas où le paramètre n et 2.n + 1 sont deux nombres premiers, le cas n = 5 devient celui à traiter en priorité.

Il devient nécessaire de travailler sur des anneaux de nombres réels. Celui contenant les valeurs a + √5.b n'est pas euclidien, mais une idée analogue à celle d'Eisenstein vient à bout de cette difficulté, il suffit de remplacer √5 par le nombre d'or, Dirichlet utilise une autre méthode, plus complexe qui démontre un résultat plus faible mais suffisant pour sa démonstration. La réticence des mathématiciens à utiliser ces structures provient d'une difficulté parfaitement connue à l'époque. Elles possèdent une spécificité que Dirichlet qualifie d'obstruction. Un anneau de cette nature contient trop d'unités, c'est-à-dire de nombres qui sont inversibles dans l'anneau. Celui des entiers relatifs en contient deux 1 et -1. L'anneau des entiers de Dirichlet en contient une infinité. Cette obstruction est d'ailleurs ce qui, jadis, poussa Brahmagupta à définir sa multiplication.

Dirichlet finit par la maîtriser suffisamment pour pouvoir travailler dans l'anneau (il choisit en pratique le sous-anneau de nombres de la forme a + √5.b avec a et b entiers relatifs). En 1825, il acquiert une célébrité instantanée grâce à un apport majeur dans la résolution du grand théorème si le paramètre est égal à cinq. La démonstration est soumise à l'académie des sciences et Adrien-Marie Legendre est nommé référé. Il lui suffit de quelques mois pour finaliser le travail de Dirichlet.