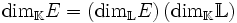Exemples d'espaces vectoriels - Définition
La liste des auteurs de cet article est disponible ici.
Espace vectoriel des polynômes
à une indéterminée
L'ensemble des polynômes à coefficients dans


![\mathbb{K}[X]](https://static.techno-science.net/illustration/Definitions/autres/a/a54a58150f8fbfa21e4e47bea7551681_74473e1ff482d8b2fb4406e56cad5749.png)
![\mathbb{K}_n[X]](https://static.techno-science.net/illustration/Definitions/autres/a/a3daa7b7e47f69202246c9e697f51678_d40ede3d3b8c23fcff8e9e411d04c553.png)
La base canonique de cet espace est une base monomiale.
à plusieurs indéterminées
L'ensemble des polynômes à plusieurs indéterminées à coefficients dans


![\mathbb{K}[X_1, X_2, \ldots, X_n]](https://static.techno-science.net/illustration/Definitions/autres/f/f4165abfb1c1fdc9ef93bd8328e48e48_d1b192d658c1aee3d54501d022a9e710.png)
Voyez aussi: l'anneau des polynômes
Extensions de corps
Supposons que

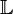
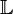






Si E est un espace vectoriel sur
Par exemple