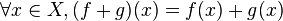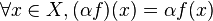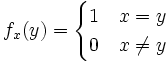Exemples d'espaces vectoriels - Définition

Espaces fonctionnels

Voyez l'article principal à la page espace fonctionnel, et plus particulièrement la section intitulée analyse fonctionnelle.

Soit X un ensemble quelconque et E un espace vectoriel arbitraire sur . L'ensemble de toutes les applications de X dans E est un espace vectoriel sur avec l'addition et la multiplication par un scalaire des fonctions.

Ces lois sont définies de la manière suivante: considérons et deux fonctions, et on a

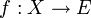
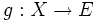
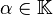
où les lois + et . apparaissant dans le second membre sont celle de E. Le vecteur nul est la fonction constante nulle envoyant tout les éléments de X sur le vecteur nul de E.

Si X est fini et E est un espace vectoriel de dimension finie alors l'espace vectoriel des fonctions de X dans E est de dimension , sinon l'espace vectoriel est de dimension infinie (non dénombrable si X est infini).

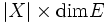
Beaucoup d'espaces vectoriels considérés en mathématiques sont des sous-espaces d'espaces fonctionnels. Donnons d'autres exemples.

Généralisation des espaces de suites à support fini

Soit X un ensemble quelconque. Considérons l'espace vectoriel F de toutes les applications de X dans qui s'annulent partout sauf en nombre fini de points de X.

Alors F est un sous-espace vectoriel de l'espace vectoriel de toutes les applications de X vers . Pour le voir, remarquez que la réunion de deux ensembles finis est finie et ainsi la somme de deux applications de F s'annulera encore en un nombre fini de points.

Si X est l'ensemble des entiers compris entre 1 et n alors cet espace peut facilement être assimilé à l'espace des n-uplets . De façon similaire, si X est l'ensemble des entiers naturels , alors cet espace n'est autre que .

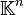
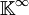
Une base naturelle de F est l'ensemble des fonctions f_x où x appartient à X, telles que

La dimension de F est ainsi égal au cardinal de X. De cette façon, nous pouvons construire un espace vectoriel de n'importe quelle dimension sur n'importe quel corps. De plus tout espace vectoriel est isomorphe à un espace vectoriel de cette forme. Tout choix d'une base détermine un isomorphisme en envoyant cette base sur une base déterminée de F.

Applications linéaires

Un exemple important issu de l'algèbre linéaire est l'espace vectoriel des applications linéaires. Soit l'ensemble des applications linéaires de E dans F (E et F étant des espaces vectoriels sur le même corps commutatif ). Alors est un sous-espace vectoriel de l'espace des applications de E vers F puisqu'il est stable pour l'addition et la multiplication par un scalaire.

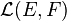
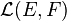
Remarquons que peut être identifié à l'espace vectoriel des matrices de manière naturelle. En fait, en choisissant une base appropriée des espaces vectoriels de dimension finie E et F, peut aussi être identifié à . Cette identification dépend naturellement du choix des bases.

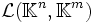
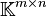
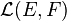
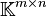
Applications continues

Si X est un espace topologique, tel que l'intervalle unité [0,1], alors nous pouvons considérer l'espace vectoriel des applications continues de X dans . C'est un sous-espace vectoriel de toutes les fonctions réelles définies sur X puisque la somme de deux applications continues quelconques est continue et la produit par un scalaire d'une application continue est continue.

Équations différentielles

Le sous-ensemble de l'espace vectoriel des applications de dans formé d'applications satisfaisant des équations différentielles linéaires est aussi un sous-espace vectoriel de ce dernier. Cela vient du fait que la dérivation est une application linéaire, c'est-à-dire (af + bg)' = af' + bg' où ' désigne cette application linéaire (aussi appelée opérateur linéaire).