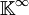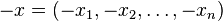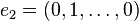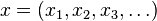Exemples d'espaces vectoriels - Définition

Introduction

Cette page présente une liste d'exemples d'espaces vectoriels. Vous pouvez consulter l'article espace vectoriel pour y trouver les définitions des notions employées ci-dessous.

Voyez également les articles sur la dimension, les bases.

Nous noterons un corps commutatif arbitraire tel que celui des réels ou celui des complexes .

Espace vectoriel trivial ou nul

L'exemple le plus simple d'espace vectoriel est l'espace nul {0}, qui ne contient que le vecteur nul (voir l'axiome 3. des espaces vectoriels). L'addition vectorielle et la multiplication par un scalaire sont triviales. Une base de cet espace vectoriel est l'ensemble vide, ainsi {0} est l'espace vectoriel de dimension 0 sur . Tout espace vectoriel sur contient un sous-espace vectoriel isomorphe à celui-ci.

Espace des n-uplets

L'exemple le plus important d'espace vectoriel est sans doute celui qui suit. Pour tout entier naturel strictement positif n, l'ensemble des n-uplets d'éléments de forme un espace vectoriel de dimension n sur appelé l'espace des n-uplets, noté . Un élément de s'écrit:

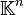
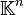
où chaque x_i est un élément de . Les opérations sur sont définies par:

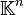
L'élément neutre pour l'addition est :

et l'opposé d'un élément : est le vecteur

Les cas les plus fréquents sont ceux où est ou bien le corps des nombres réels donnant l'espace euclidien , ou bien le corps des nombres complexes donnant .

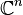
Les ensembles des quaternions et des octonions sont respectivement des espaces vectoriels de dimension quatre et huit sur le corps des nombres réels.

L'espace vectoriel est généralement muni d'une base naturelle appelée base canonique:

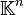
où 1 désigne l'élément neutre multiplicatif de .

Le corps

Le prochain exemple simple est le corps lui-même. L'addition vectorielle est simplement l'addition du corps et la multiplication par un scalaire est la multiplication du corps. L'élément neutre de pour la multiplication forme une base de et ainsi est un espace vectoriel de dimension 1 sur lui-même.

a seulement deux sous-espaces { 0 } et lui-même.

Matrices

Soit l'ensemble des matrices à coefficients dans . Alors muni de l'addition des matrices et la multiplication par un scalaire des matrices (consistant à multiplier chaque coefficient par un même scalaire) est un espace vectoriel sur . Le vecteur nul n'est autre que la matrice nulle. La dimension de est égale à mn.

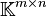
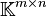
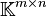
La base canonique est la base formée par les matrices ayant un seul coefficient égal à 1 et tous les autres coefficients égaux à 0.

Espace des suites à support fini

Soit l'ensemble des suites infinies d'éléments de telles que seul un nombre fini d'éléments soit non nul. Plus précisément, si nous écrivons un élément de sous la forme:

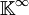
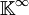
alors seulement un nombre fini des nombres x_i est non nul (autrement dit les coordonnées du vecteur x deviennent nulles à partir d'un certain rang).

L'addition et la multiplication par un scalaire sont alors définies comme sur l'espace vectoriel des n-uplets.

L'ensemble est un espace vectoriel de dimension infinie dénombrable. La base canonique est celle formée par les vecteurs qui comportent un 1 à la ième place et des zéros partout ailleurs.

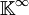
Cet espace vectoriel est le coproduit d'un nombre dénombrable de copies de l'espace vectoriel .

Remarquez le rôle de la condition de finitude ici. Nous pourrions considérer des suites arbitraires d'élements de , qui constituent aussi un espace vectoriel (souvent noté ).

Cependant la dimension de cet espace est infinie non dénombrable et il n'y a pas de choix évident de bases. Puisque les dimensions sont distinctes, l'espace vectoriel des suites de n'est pas isomorphe à . Cet espace vectoriel est le produit d'un nombre dénombrable de copies de .

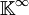
Il vaut la peine de noter que est l'espace dual de . Ainsi, dans la comparaison au cas rigide de la dimension finie, nous voyons qu'un espace vectoriel de dimension infinie n'a nul besoin d'être isomorphe à son dual (et encore moins d'être isomorphe à son bidual).