Fonction de Wannier - Définition

Propriétés générales

Sur la base de la définition la plus simple exprimée ci-dessus, les propriétés suivantes ont été démontrées :

• Pour tout vecteur R'  :

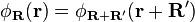
En d'autres termes, une fonction de Wannier dépend uniquement du vecteur (r-R). En conséquence, ces fonctions sont parfois écrites sous la notation alternative :

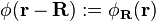
• Les fonctions de Bloch peuvent s'écrire en termes de fonctions de Wannier de la manière suivante :

,

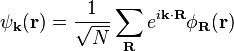
où la sommation se fait sur chaque vecteur R du réseau cristallin.

• L'ensemble des fonctions d'onde est une base orthonormée pour la bande considérée.

Il est généralement considéré que la fonction est localisée autour du point R, et décroît rapidement vers zéro dès que l'on s'éloigne de ce point. Cependant, prouver et quantifier cette assertion peut être difficile, et constitue toujours le sujet de recherches.

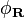
Les fonctions de Wannier ont été également appliquées aux potentiels quasi-périodiques.