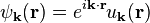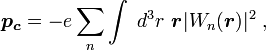Fonction de Wannier - Définition

Introduction

Exemple de fonction de Wannier dans le titanate de baryum.

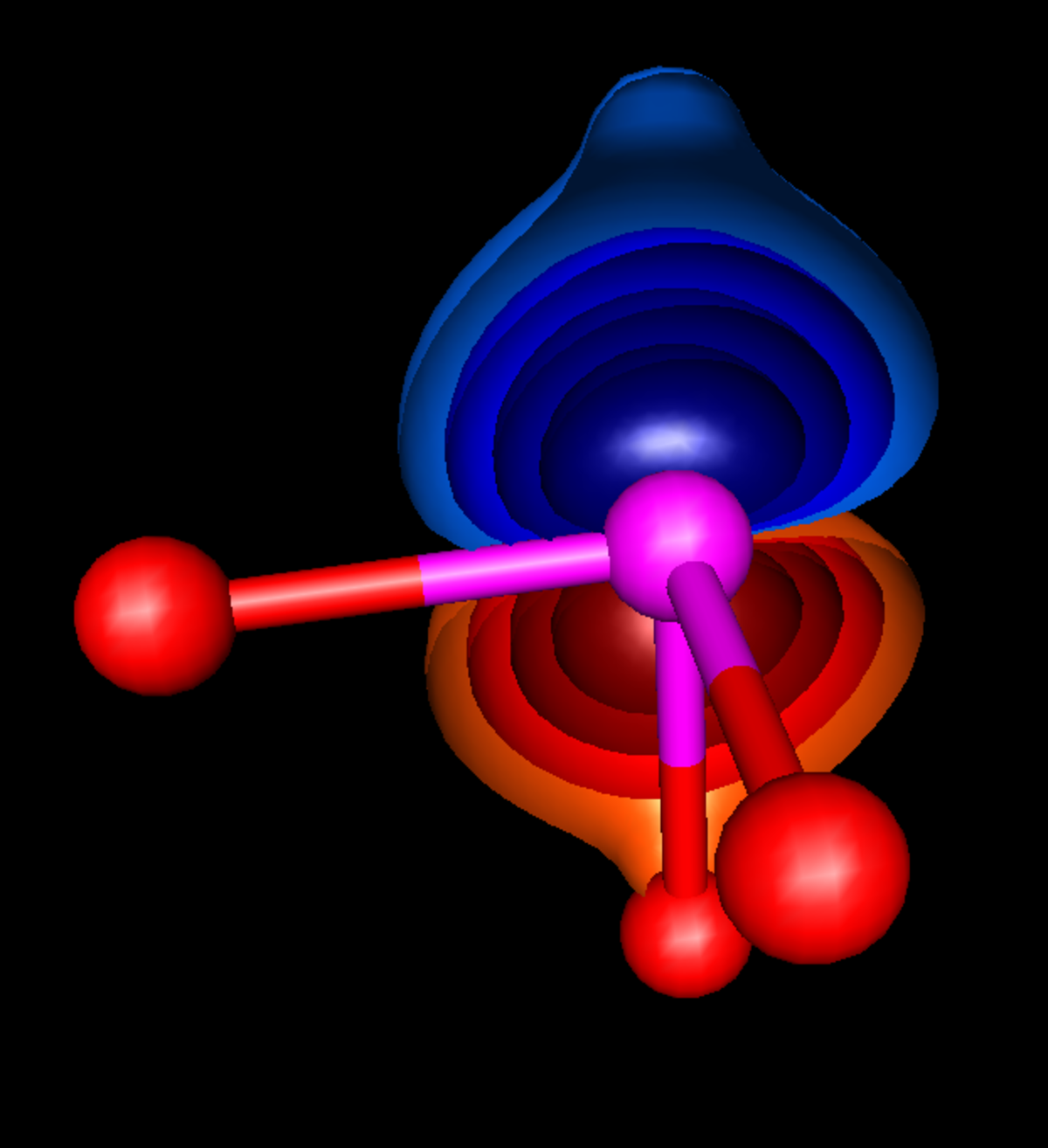
Les fonctions de Wannier constituent un ensemble complet de fonctions orthogonales utilisé en physique du solide. Elles ont été introduites dans la discipline par le physicien suisse Gregory Wannier.
Les fonctions de Wannier pour différents sites d'un réseau cristallin sont orthogonales, constituant une base ad-hoc pour le développement des états électroniques dans certains régimes. Ces fonctions ont un usage varié et important, comme par exemple dans l'analyse des forces de liaison agissant sur les électrons. On a prouvé qu'elles sont en général localisées, au moins pour les isolants. Ces fonctions sont aussi utilisées de manière spécifique dans l'analyse des excitons et de la matière condensée de Rydberg.

Définition

Bien que les fonctions de Wannier puissent être choisies de nombreuses manières, la définition la plus simple et la plus commune en physique de l'état solide est la définition originale, qui se présente de la manière suivante.
On choisit une bande d'un cristal parfait, et on écrit ses états de Bloch comme :

où est une fonction de même périodicité que le cristal. Les fonctions de Wannier sont alors définies par la relation :

,

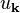
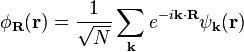
dans laquelle :

• R est un vecteur du réseau cristallin (ce qui implique qu'il existe une fonction de Wannier pour chacun de ces vecteurs).
• N est le nombre de mailles primitives dans le cristal.
• la somme sur les k comprend tous les valeurs des k dans la zone de Brillouin (ou toute autre maille primitive du réseau réciproque) cohérentes avec les conditions périodiques aux limites du cristal. Cela inclut N valeurs différentes de k, réparties régulièrement dans la zone de Brillouin. N étant de manière usuelle très grand, la somme peut alors être écrite comme une intégrale selon la règle de remplacement :

,

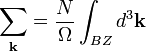
où BZ désigne la zone de Brillouin, de volume Ω.

Les fonctions de Wannier peuvent être considérées comme une extension de l'approximation des liaisons fortes aux fonctions de Bloch, les fonctions d'onde dégénérées satisfaisant à la condition de Bloch s'écrivant : , où k parcourt les N valeurs de la preière zone de Brillouin compatibles avec les conditions aux limites de Born-von Karman. Les fonctions de Wannier peuvent alors être définies pour toutes les bandes que celles-ci soient ou non correctement décrites dans le cadre de l'approximation des liaisons fortes. Cependant, si la bande que l'on cherche à décrire n'est pas une bande de liaisons fortes étroite, les fonctions de Wannier correspondantes ne présentent plus de formes similaires ax fonctions d'ondes électroniques des atomes isolés.

Applications

Application en théorie moderne de la polarisation

Les fonctions de Wannier ont été récemment appliquées dans la description de la polarisation dans les cristaux (matériaux ferroélectriques, par exemple). On pourra se référer en particulier à l'introduction sur le sujet donnée par David Vanderbilt.
La polarisation par maille unitaire dans un solide peut être définie comme le moment dipolaire de la densité de charge de Wannier :

où l'intégration se fait sur les bandes occupées, et W_n est la fonction de Wannier localise dans la maille pour la bande n. La modification de la polarisation durant un processus physique continu est obtenu par la dérivée temporelle de la polarisation et peut être également formulée en termes de la phase de Berry des états de Bloch occupés.

Développement d'une théorie du transport