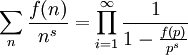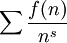Fonction multiplicative - Définition
La liste des auteurs de cet article est disponible ici.
Séries de Dirichlet
Produit de convolution
Si f et g sont deux fonctions multiplicatives, on définit une nouvelle fonction multiplicative f * g, appelée convolution de Dirichlet de f et g, comme suit :
-
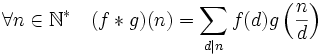
où la somme portant sur tous les diviseurs positifs d de n.
En effet, introduisons n et m deux entiers premiers entre eux. Leurs décompositions en facteurs premiers ne comportent aucun nombre premier commun. Si d est un diviseur de n.m, alors tout diviseur premier p de d divise n.m et donc par le lemme d'Euclide ou bien n ou bien m. Par regroupement de facteurs premiers, l'entier d s'écrit de manière unique d=d1.d2 comme produit de deux nombres entiers premiers d1 etd2 divisant respectivement n et m. Par définition :
-
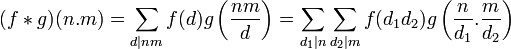
Or, comme f et g sont elles-mêmes supposées multiplicatives :
-
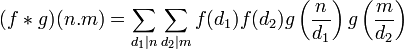
-
![(f*g)(n.m)=\left[\sum_{d_1|n}f(d_1)g\left(\frac{n}{d_1}\right)\right].\left[\sum_{d_2|m}f(d_2)g\left(\frac{m}{d_2}\right)\right]](https://static.techno-science.net/illustration/Definitions/autres/e/ebee37f3ad93f544e890f3ab57098540_23eda3c8a9cc1c31bb738b14366fdebf.png)
- (f * g)(n.m) = (f * g)(n).(f * g)(m).
C'est précisément l'égalité attendue.
Avec cette opération, l'ensemble de toutes les fonctions multiplicatives se transforme en groupe abélien; l'élément neutre est ε.
Les relations les plus importantes vérifiées par les fonctions multiplicatives listées ci-dessus sont :
- ε = μ * 1 (la formule d'inversion de Möbius)
- φ = μ * Id
- d = 1 * 1
- σ = Id * 1 = φ * d
- σk = Idk * 1
- Id = φ * 1 = σ * μ
- Idk = σk * μ
Anneau de Dirichlet
La convolution de Dirichlet peut être définie pour des fonctions arithmétiques générales, et leur confère une structure d'anneau, l'anneau de Dirichlet.
Formellement, à une fonction arithmétique f est associée une série formelle :
Pour une fonction complètement multiplicative :
-
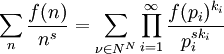
-
![\sum_n \frac{f(n)}{n^s}=\prod_{i=1}^{\infty}\sum_{k=0}^{\infty}{\left[\frac{f(p)}{p^s}\right]}^s](https://static.techno-science.net/illustration/Definitions/autres/5/5d79230bccae59065a1ba92134445676_edad911ef5936e327ea80f2f12286766.png)
-