Convolution de Dirichlet - Définition

Introduction

En mathématiques, la convolution de Dirichlet, encore appelée produit de convolution de Dirichlet ou produit de Dirichlet est une loi de composition interne définie sur l'ensemble des fonctions arithmétiques, c'est-à-dire des fonctions définies sur les entiers strictement positifs et à valeurs dans les nombres complexes. Cette loi de convolution est utilisée en arithmétique, aussi bien algébrique qu'analytique. On la trouve aussi pour résoudre des questions de dénombrements.

Le mathématicien Johann Peter Gustav Lejeune Dirichlet développe ce produit en 1837 pour démontrer le théorème de la progression arithmétique.

Définition, exemples et premières propriétés

Définition

• La convolution de Dirichlet de deux fonctions arithmétiques f et g, est la fonction, généralement notée f * g définie par :

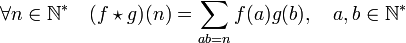
Exemples

Si f est la fonction 1_F, c'est-à-dire celle qui vaut 0 partout sauf en 1 où elle vaut 1, et si g est une fonction arithmétique quelconque, on dispose de l'égalité :

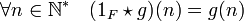
L'ensemble F des fonctions arithmétiques admet un élément neutre, la fonction 1_F.

Si φ désigne l'indicatrice d'Euler, Id la fonction identité, qui à n associe n et c₁ la fonction constante 1, on dispose de l'égalité :

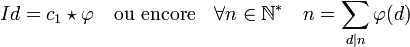
Ici, les symboles d|n désignent l'ensemble des diviseurs entiers positifs de n.

Premières propriétés

Dans toute la suite de l'article F désigne l'ensemble des fonctions arithmétiques. La convolution de Dirichlet possède des propriétés communes à beaucoup de lois de composition internes :

• La convolution de Dirichlet est commutative :

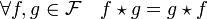
Cette propriété est une conséquence directe de la définition.

• La convolution de Dirichlet est associative :

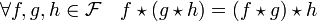
La démonstration provient du caractère symétrique de la formulation suivante :

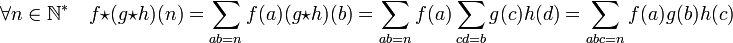
• La convolution de Dirichlet est distributive par rapport à l'addition :

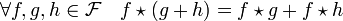
La démonstration est aussi élémentaire que la précédente :

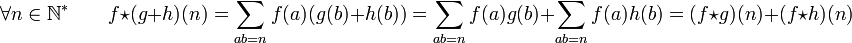
Le premier exemple montre que :

• La convolution de Dirichlet admet un élément neutre, c'est la fonction partout nulle sauf en 1 où elle vaut 1.

Dans la suite de l'article, l'élément neutre est noté 1_F.

Il est possible de résumer ces différentes propriétés par :

• L'ensemble F des fonctions arithmétiques munis de l'addition et de la convolution de Dirichlet forme un anneau commutatif unitaire.

Unitaire signifie ici que l'anneau contient un élément neutre pour la deuxième loi de composition interne.

Série L de Dirichlet

Si f est une fonction arithmétique, on définit sa série L (série de Dirichlet) par

pour les arguments complexes s pour lesquels la série converge (s'il en existe). La multiplication des séries L est compatible avec la convolution de Dirichlet dans le sens suivant :

pour tous les s pour lesquels les deux séries du côté gauche convergent, l'une des deux en tout cas convergeant ABSOLUMENT (Noter que la simple convergence des deux séries à gauche N'IMPLIQUE PAS celle de la série à droite!). Ceci est ressemblant au théorème de convolution si on pense aux séries L comme une transformation de Fourier.