Graphe de Gran - Définition
La liste des auteurs de cet article est disponible ici.
Calibration d'électrode
L'analyse de données potentiométriques nécessite la connaissance préalable de
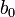
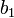
Si l'électrode est mal calibré, une correction de décalage peut être calculée in situ à partir de la pente en milieu acide:
- Pour un titrage d'un acide par de la base, la pente du côté acide est
![-[OH^-]_{0^{ }}10^b](https://static.techno-science.net/illustration/Definitions/autres/2/21af90ac1c6fd99ba3ab2691deccbc04_73b0ec56e9e64a74dc3811cb85b2109b.png)
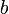
![[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a6768ed3c004ea99b7818ac314e0f47c_2bc6b5bf1ee0d64d78cdeab54c7c3776.png)
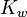
- Pour un titrage d'une base par de l'acide, telle qu'illustré dans les exemples, la pente du côté acide,
![[H^+]_{0^{ }}10^b](https://static.techno-science.net/illustration/Definitions/autres/5/53b1088eb3e7a9a3b7e16c91582d816f_fce4364be03eb7b7c25a8ab4d8f330b2.png)
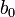
![-[H^+]_{0^{ }}10^{-b_0}/K_w](https://static.techno-science.net/illustration/Definitions/autres/6/6d6b6359e7198c7c5e74712ad200d4db_c9245e24be2966f4be9bded74db24836.png)
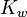
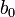
La valeur de
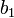
![[H^{+_{ }}]_i](https://static.techno-science.net/illustration/Definitions/autres/2/2f59218efd4a9d1946146351979b9c77_4505588f5fbb2c47f3cc52c3961c003d.png)
![[H^+_{ }]_0](https://static.techno-science.net/illustration/Definitions/autres/1/172ef49fe7646351a7adcd0a1e1044ca_1f576cfc2712c7af1af828bdf9a84948.png)
![[OH^-_{ }]_0](https://static.techno-science.net/illustration/Definitions/autres/3/38ac1351a97dbf42ebca61d922c1ae9b_cd2f4d50a0dc4e7de837a3eaf6647433.png)
Suivant le travail antérieur de McBryde (1969), Gans et O'Sullivan (2000) décrivent une approche itérative pour calculer
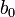
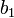
![-log_{10}[H^+]_i = b_0 - b_1E_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/8/8ace3adcb223ae4b60459411a2532324_54819b7deb7e6f9d78223914590f7d61.png)
-
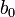
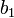
- on trace des fonctions Gran modifiées, soit
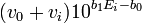
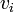
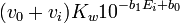
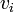
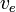
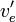
- comme auparavant, la différence entre ces volumes d'équivalence servent à estimer le mais aussi pour calculer une 'concentration effective' de la base
![v_e [OH^-]_{0^{ }}/v_e^{\prime}](https://static.techno-science.net/illustration/Definitions/autres/d/da863bd7a2acd549312c84e9a714a79b_245005474e8985287be072fbf191bd5b.png)
- les valeurs approximatives de
![[H^+]_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a0d788dce843b9fd9b813de4d5cc407b_0e027fd126a469b1d972eef8987d6ef4.png)
![(v_{0^{ }} [H^+]_0-v_i[OH^-]_0)/(v_0+v_i)](https://static.techno-science.net/illustration/Definitions/autres/9/9136d4a19abbbf26fa6d0247750cee8d_0f07a0fc0a111348c937bbe3ea2482ab.png)
![(v_e [H^+]_0-v_i v_e[OH^-]_0 /v_e^{\prime})/(v_0+v_i)](https://static.techno-science.net/illustration/Definitions/autres/d/db68b7849cb90d89198a1ba5bd939ac3_a2ec0308ea6290e6b1c9dc35559904ca.png)
- la définition
![-log_{10}[H^+]_i = b_0 - b_1E_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/8/8ace3adcb223ae4b60459411a2532324_54819b7deb7e6f9d78223914590f7d61.png)
![E_{i^{ }} = b_0/b_1 + (1/b_1)log_{10}[H^+]_i](https://static.techno-science.net/illustration/Definitions/autres/c/cf94c3bee481bea0cfdec4364e02a6a1_1e45e43e028421b4110fedd96fb6b226.png)
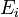
![log_{10}[H^+]_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/4/4a67babbe361c935555bfd70b91a39ae_323d5d9b71af9ef0a99563636ab4cff2.png)
![[H^+]_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a0d788dce843b9fd9b813de4d5cc407b_0e027fd126a469b1d972eef8987d6ef4.png)
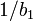
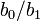
- les étapes 2 et 3 sont répétées avec les nouvelles valeurs de
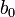
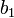
Cette procédure pourrait en principe être modifiée pour des titrages de base par de l'acide. Le logiciel GLEE (nom dérivé de 'GLass Electrode Evaluation') met en œuvre cette approche pour l'étallonage d'un électrode à partir d'un titrage d'acide fort par une base forte. Ce logiciel peut aussi calculer (par un procédé non-linéaire de moindres carrés séparé) une 'correction' de la concentration de la base. L'avantage de cette méthode est que la calibration peut être conduite dans le même milieu à force ionique constante que l'on utilisera pour la détermination des constantes d'équilibre.
Il est à noter que les fonctions de Gran habituelles donnent aussi les volumes d'équivalence requis et que, comme
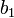
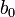
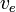
![[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a6768ed3c004ea99b7818ac314e0f47c_2bc6b5bf1ee0d64d78cdeab54c7c3776.png)
![[H^+]_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a0d788dce843b9fd9b813de4d5cc407b_0e027fd126a469b1d972eef8987d6ef4.png)
![(v_{0{^{ }}} [H^+]_0-v_i[OH^-]_0)/(v_0+v_i) = [H^+]_i - K_w/[H^+]_i](https://static.techno-science.net/illustration/Definitions/autres/7/705854d77c5212c7d671721085eed406_0c89ef45d223abbc86d7e99c0d361b54.png)

















































