Graphe de Gran - Définition
La liste des auteurs de cet article est disponible ici.
Titrage de base forte par acide fort
Des graphes miroitant les précédents sont obtenus avec un titrage de base forte par acide fort, et les pentes sont renversées.
![\frac{v_0 [OH^-]_0-v_i[H^+]_0}{v_0+v_i} \begin{cases} \approx [OH^-]_i \text{ ou } K_w 10^{pH_i} & \text{ si } v_{0^{ }} [OH^-]_0 > v_i[H^+]_0 \mathrm{ ~(r \acute e gion~alcaline)} \\ = 0 & \text{ si } v_{0^{ }} [OH^-]_0 = v_i[H^+]_0 \mathrm{ ~(point~d' \acute e quivalence)} \\ \approx -[H^+]_i \text{ ou } -10^{-pH_i} & \text{ si } v_{0^{ }} [OH^-]_0 < v_i[H^+]_0 \mathrm{ ~(r \acute e gion~acide)} \end{cases}](https://upload.wikimedia.org/math/d/a/d/dadd7664a6aa0d28907b4b820ccc403b.png)
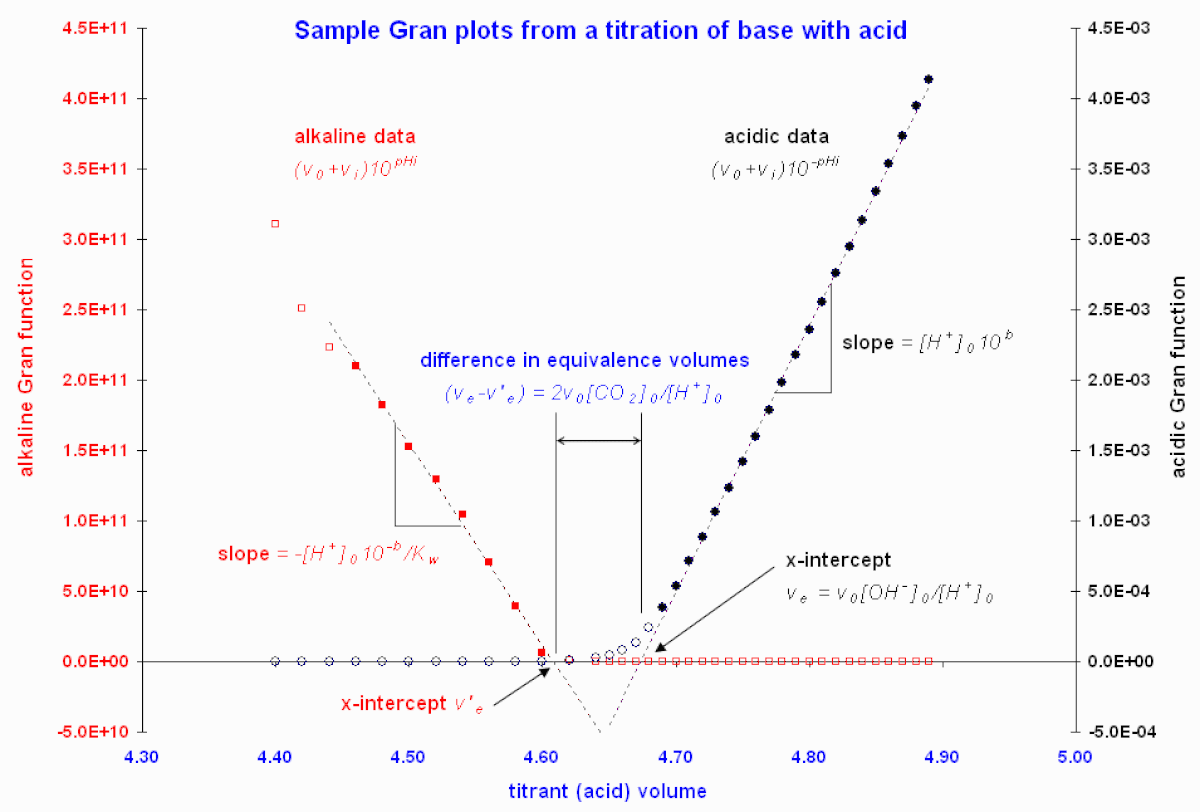
Figure 1. graphes de Gran illustratifs à partir des données de Butler (1998). Les cercles emplis indiquent les points retenus pour le calcul de l'intercepte par la méthode des moindres carrées donnant les courbes pointillées.
Donc,

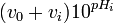
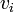
![-[H^+]_0/K_{w^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a4b3dbe3e9f4730ccb571e559010d239_ed4c115663c5c89142346651385656ae.png)

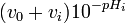
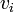
![[H^+]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/8/8144701b6d4768b0f84f6395ac6373c6_ad9d15aeea917f83e47d504bf784946d.png)

![v_e=v_0 [OH^-]_{0^{ }}/[H^+]_0](https://static.techno-science.net/illustration/Definitions/autres/2/233b891824c3aa2fbc69e919629eeb89_83f3aa73630ab2ee8382679a217a669b.png)
La Figure 1 présente des graphes de Gran suite à un titrage d'une base forte par un acide fort.
Contrôle potentiométrique de H+
Pour utiliser des mesures potentiométriques
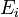
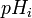
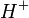
![-log_{10}[H^+]_i = b_0 - b_1E_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/8/8ace3adcb223ae4b60459411a2532324_54819b7deb7e6f9d78223914590f7d61.png)
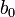
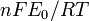
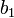
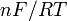
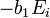
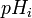
Ainsi, comme vu plus tôt pour un titrage d'acide fort par une base forte,

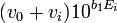
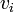
![-10^{b_0}[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/3/3de0b924228585866847cb713e348e62_decb52a8587608f9befa3f4a6e71acae.png)

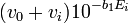
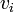
![10^{-b_0}[OH^-]_0/K_{w^{ }}](https://static.techno-science.net/illustration/Definitions/autres/b/ba6f40ac5fa17a706f8acf5186caadea_3d05bfc088ffa56d001c59e9c6cb8b9f.png)

![v_e=v_0 [H^+]_0/[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/f/fa8f22bf3df8051351474ba8990a1d2d_abb8c0bafbe7e379df08f02f2a3d66d0.png)
Des graphiques analogues peuvent être construits avec les données d'un titrage d'une base par de l'acide.
Contenu en carbonate
Martell et Motekaitis (1992) ont utilisé les régions les plus linéaires pour leurs graphes, puis exploité la différence entre le volume d'équivalence mesuré du côté acide et celui mesuré du côté alcalin pour ainsi estimer la quantité de CO2 absorbée par la solution alcaline. Ce processus est illustré dans la Figure 1. Dans ce cas, l'acide supplémentaire qui sert à neutraliser le carbonate, par double protonation, dans un volume
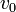
![(v_e-v_e^{\prime})[H^+]_{0^{ }} = 2v_0[CO_2]_0](https://static.techno-science.net/illustration/Definitions/autres/9/996256dcdb9e670f560448c0df504148_7f91e6060b14782887d400d9c763493a.png)
![(v_e^{\prime}-v_e)[OH^-]_{0^{ }} = 2v_e^{\prime}[CO_2]_0](https://static.techno-science.net/illustration/Definitions/autres/6/60f7596e6644addd29d7df1f6e8aeeb9_cefbca77dd20fa78bcd4f7ad65ea02a3.png)
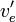
Quand le contenu total de CO2 absorbé est important, tel que dans les eaux naturelles et les effluents alcalins, deux ou trois inflections peuvent être décelées dans la courbe pH-volume dues aux effets tampons qu'ont le bicarbonate et le carbonate en concentrations importantes. Comme l'ont discuté Stumm et Morgan (1981), l'analyse de telles eaux peut mettre en œuvre jusqu'à six graphes de Gran à partir d'une seule titrage pour estimer les multiples points d'équivalence et mesurer l'alcalinité totale et les concentrations de carbonate et/ou de bicarbonate.
Contrôle potentiométrique d'autres espèces
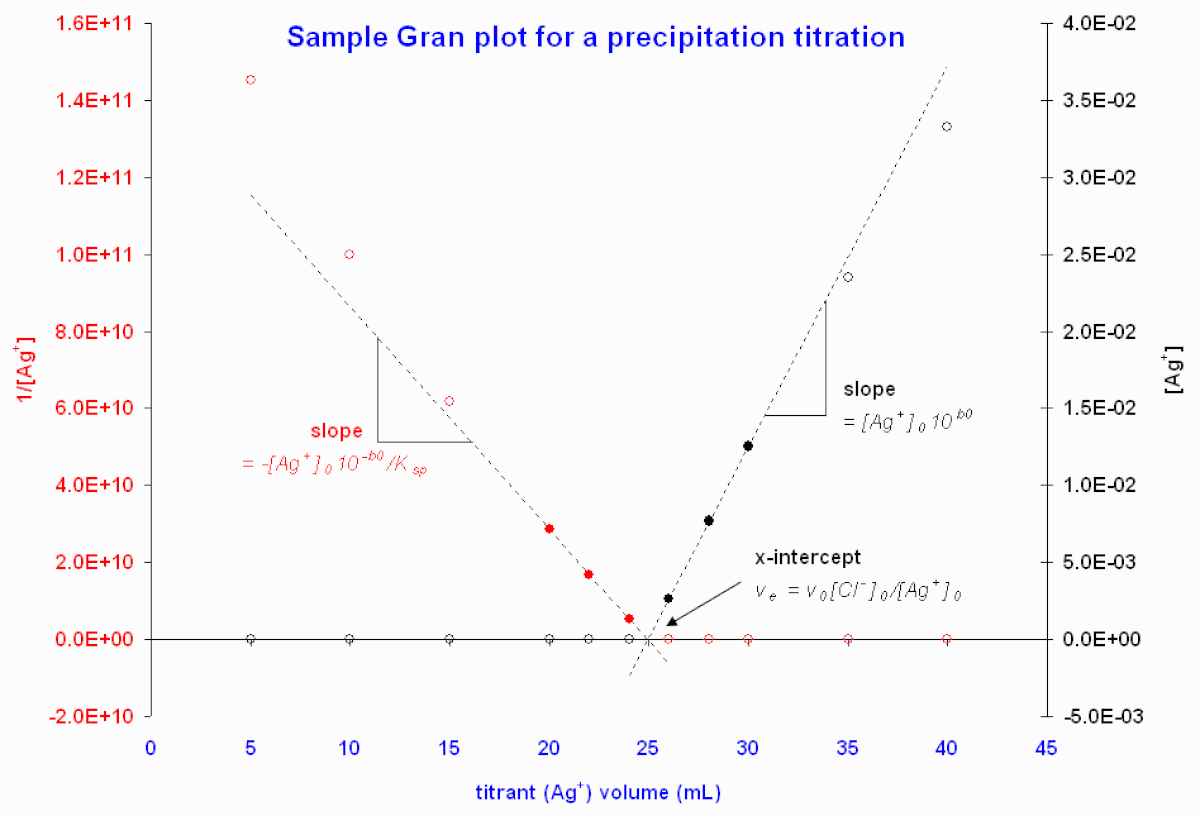
Figure 3. graphes de Gran illustratifs à partir des données d'un titrage de Cl- par Ag+ avec contrôle potentiométrique. Les potentiels ont été converties en valeurs de [Ag+]. Les cercles emplis indiquent les points retenus pour le calcul de l'intercepte par la méthode des moindres carrées donnant les courbes pointillées.
Lorsque l'on contrôle une autre espèce, disons
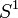
![-log_{10}[S^1]_i = b_0 - b_1E_{i^{ }}](https://static.techno-science.net/illustration/Definitions/autres/e/e84bf6c171418f95a8de196bf3397904_16116e122290bb38a1a89213576d576f.png)
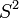
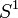
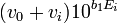
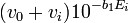
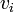
![v_0 [S^0]_0 /[S^1]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/6/63f75ebe9f0d20cf06d925b6fa4dbff8_180a4c126812944429b57c3b8433f445.png)
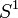
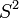
![v_0 [S^1]_0 /[S^0]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/1/185050ed1788ea38127878cd6f004625_e5b0894bafb1aa245cbff971805ac72d.png)
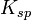
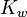
Pour illustrer ceci, prenons l'exemple d'un titrage potentiométrique de Cl- par Ag+: ![\frac{v_0 [Cl^-]_0-v_i[Ag^+]_0}{v_0+v_i} \begin{cases} \approx [Cl^-]_i \text{ ou } K_{sp} 10^{-b_1E_i+b_0} & \text{ lorsque } v_{0^{ }} [Cl^-]_0 > v_i[Ag^+]_0 \mathrm{ ~(avant~l' \acute e quivalence)} \\ = 0 & \text{ lorsque } v_{0^{ }} [Cl^-]_0 = v_i[Ag^+]_0 \mathrm{ ~(\grave a ~l' \acute e quivalence)} \\ \approx -[Ag^+]_i \text{ ou } -10^{b_1E_i-b_0} & \text{ lorsque } v_{0^{ }} [Cl^-]_0 < v_i[Ag^+]_0 \mathrm{ ~(apr \grave es ~l' \acute e quivalence)} \end{cases}](https://upload.wikimedia.org/math/3/4/b/34b6f849f6a036f20fd8a01e1b5325b7.png)
Donc,

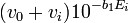
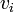
![-[Ag^+]_010^{-b_0}/K_{sp^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a823b3dc4380087ad7d9b224c1d2f242_4abfcf098156c8fb5531e09dcb6399b1.png)

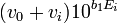
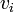
![[Ag^+]_{0^{ }}10^{b_0}](https://static.techno-science.net/illustration/Definitions/autres/1/17e9d5eaf394597e1ff33e8544071407_bfcd6e0cc2b19a657f48c176cf50ca06.png)

![v_e=v_0 [Cl^-]_{0^{ }}/[Ag^+]_0](https://static.techno-science.net/illustration/Definitions/autres/f/f28f4a6a774f654a527b714d7269023a_b530701a4f72e9045c270c84a5268fe0.png)
La Figure 3 donne un exemple de données potentiométriques d'un tel titrage.

















































