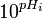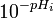Graphe de Gran - Définition

Littérature citée

• Buffle, J., Parthasarathy, N. et Monnier, D. (1972): Errors in the Gran addition method. Part I. Theoretical Calculation of Statistical Errors; Anal. Chim. Acta 59, 427-438; Buffle, J. (1972): Anal. Chim. Acta 59, 439.
• Butler, J. N. (1991): Carbon Dioxide Equilibria and Their Applications; CRC Press: Boca Raton, FL.
• Butler, J. N. (1998): Ionic Equilibrium: Solubility and pH Calculations; Wiley-Interscience. Chap. 3.
• Gans, P. et O'Sullivan, B. (2000): GLEE, a new computer program for glass electrode calibration; Talanta, 51, 33–37.
• Gran, G. (1950): Determination of the equivalence point in potentiometric titrages, Acta Chem. Scand., 4, 559-577.
• Gran, G. (1952): Determination of the equivalence point in potentiometric titrages-- Part II, Analyst, 77, 661-671.
• Gran, G., Johansson, A. et Johansson, S. (1981): Automatic titrage by Stepwise Addition of Equal Volumes of Titrant Part VII. Potentiometric Precipitation titrages, Analyst, 106, 1109-1118.
• Harris, D. C.: Quantitative Chemical Analysis, 5th Ed.; W.H. Freeman & Co., New. York, NY, 1998.
• Martell, A. E. et Motekaitis, R. J.: The determination and use of stability constants, Wiley-VCH, 1992.
• McBryde, W. A. E. (1969): Analyst, 94, 337.
• Rossotti, F. J. C. et Rossotti, H. (1965): J. Chem. Ed., 42, 375
• Skoog, D. A., West, D. M., Holler, F. J. et Crouch, S. R. (2003): Fundamentals of Analytical Chemistry: An Introduction, 8th Ed., Brooks and Cole, Chap. 37.
• Stumm, W. et Morgan, J. J. (1981): Aquatic chemistry, 2nd Ed.; John Wiley & Sons, New York.

Comportement non-idéal

Dans toute titrage sans espèces tampons, les graphes avant et après l'équivalence devraient idéalement croiser l'abscisse au même point, mais un comportement non-idéal peut être occasionné par des erreurs de mesures (e.g. avec un électrode mal calibré, un temps équilibration insuffisant avant d'enregistrer le potentiel, une dérive de la force ionique), des erreurs d'échantillonnage (e.g. une densité de données faible dans les régions linéaires) ou par un modèle chimique incomplet (e.g. avec la présence d'impuretés titrables telle que le dans la base, ou une précipitation incomplète lors d'un titrage potentiométrique à cause de solutions trop diluées, pour lequel cas Gran et al. (1981) propose des approches alternatives). Buffle et al. (1972) discutent de plusieurs sources de telles erreurs.

Parce que les fonctions en ou de Gran ne tendent qu'asymptotiquement vers zéro, sans jamais l'atteindre, la courbure qui résulte en approche de l'équivalence est attendue dans tous les cas. Toutefois, les praticiens ne s'accordent pas sur lesquelles données utiliser pour déterminer l'équivalence, qu'il s'agisse d'utiliser les données avant ou après l'équivalence ou des deux côtés, et qu'il s'agisse d'inclure les données les plus proches de l'équivalence ou seulement celles dans les portions les plus linéaires: Les données les plus proches de l'équivalence feront en sorte que les deux estimations de l'intercepte sur l'axe de x seront plus coïncidants et coïncideront mieux aussi aux estimés provenant des premiers ou seconds dérivés, alors que l'on peut présumer que les données à pH acide seront moins asujetties aux interférences provenant d'impuretés tamponeuses et titrables, telles que le bicarbonate et le carbonate dans la base (voir ), ainsi que de l'effet d'une force ionique dérivante. Dans les graphiques donnés ici en exemples, les régions les plus linéaires (les données représentées par les cercles emplis) étaient celles choisies pour le traitement par la méthode des moindres carrés donnant les pentes et interceptes. La sélection des données à retenir est toujours subjective.