Graphe de Gran - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un graphe de Gran (aussi méthode de Gran et titrage de Gran) est un moyen usuel d'étalonner un titrate ou un titrant en estimant le volume d'équivalence pendant une titrage d'un acide fort avec une base forte ou pendant un titrage potentiométrique. De tels graphes peuvent aussi servir à estimer le contenu en carbonate d'une solution aqueuse, ainsi que les constantes d'acidité K d'acides ou bases faibles à partir de données de titrage.
Les graphes de Gran mettent en œuvre des approximations linéaires de relations a priori non-linéaires entre la quantité mesurée, le pH ou le potentiel électromoteur (f.e.m.), et le volume de titrant ajouté. D'autres types de mesures de concentration, tels que l'absorbance spectrophotométrique ou les déplacements chimiques en RMN, peuvent en principe aussi servir. Ces approximations ne sont valides que près du point d'équivalence, mais non pas au point d'équivalence, et donc la méthode diffère des autres estimations de point d'équivalence utilisant les premiers ou seconds dérivés, méthodes qui requièrent des données au point d'équivalence. A l'origine, c'est-à-dire avant l'arrivée d'ordinateurs, les graphes de Gran ont été conçus comme détermination graphique, où un tracé sur papier quadrillé serait manuellement extrapolé pour estimer l'intercepte sur l'abscisse (l'axe du volume). Ce procédé a été depuis remplacé par l'analyse plus précise par la méthode des moindres carrés, surtout à l'aide de logiciels de feuilles de calcul qui possèdent une fonction intégrée appliquant la méthode des moindres carrées.
Titrage d'acide fort par base forte
Lors d'un titrage pH-métrique d'une solution d'acide fort, nous avons à chaque ième point,
où Kw est la constante de autoprotolyse de l'eau.
Si le volume de départ de l'acide est
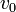
![[H^+]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/8/8144701b6d4768b0f84f6395ac6373c6_ad9d15aeea917f83e47d504bf784946d.png)
![[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a6768ed3c004ea99b7818ac314e0f47c_2bc6b5bf1ee0d64d78cdeab54c7c3776.png)
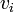
![\frac{v_0 [H^+]_0-v_i[OH^-]_0}{v_0+v_i} \begin{cases} \approx [H^+]_i \text{ ou } 10^{-pH_i} & \text{ si } v_{0^{ }} [H^+]_0 > v_i[OH^-]_0 \mathrm{ ~(r \acute e gion~acide)} \\ = 0 & \text{ si } v_{0^{ }} [H^+]_0 = v_i[OH^-]_0 \mathrm{ ~(point~d' \acute e quivalence)} \\ \approx -[OH^-]_i \text{ ou } -K_w 10^{pH_i} & \text{ si } v_{0^{ }} [H^+]_0 < v_i[OH^-]_0 \mathrm{ ~(r \acute e gion~alcaline)} \end{cases}](https://upload.wikimedia.org/math/e/4/4/e44f53c426d37417d4dddd0508e7399e.png)
Au point d'équivalence, le volume d'équivalence
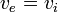
Or,
|
|
| aura une région linéaire | avant | l'équivalence, avec pente |
|
|
|
| aura une région linéaire | après | l'équivalence, avec pente |
|
|
|
| comme intercepte de l'abscisse |
Le volume d'équivalence ve est utilisé pour calculer l'inconnu, soit
![[H^+]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/8/8144701b6d4768b0f84f6395ac6373c6_ad9d15aeea917f83e47d504bf784946d.png)
![[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a6768ed3c004ea99b7818ac314e0f47c_2bc6b5bf1ee0d64d78cdeab54c7c3776.png)
Avant d'entamer le titrage, le pH-mètre est d'habitude calibré à l'aide de solutions tampons aux pH connus. La puissance ionique peut être maintenue par un choix judicieux de l'acide et de la base. Par exemple, un titrage de l'acide HCl avec la base NaOH d'à-peu-près la même concentration remplacera H+ par un ion de même charge (Na+) à plus ou moins la même concentration, pour maintenir la puissance ionique assez constante. Autrement, on peut utiliser une concentration relativement élevée d'électrolyte de fond, ou le coefficient d'activité peut être calculé.
Concentrations et constantes de dissociation d'acides faibles
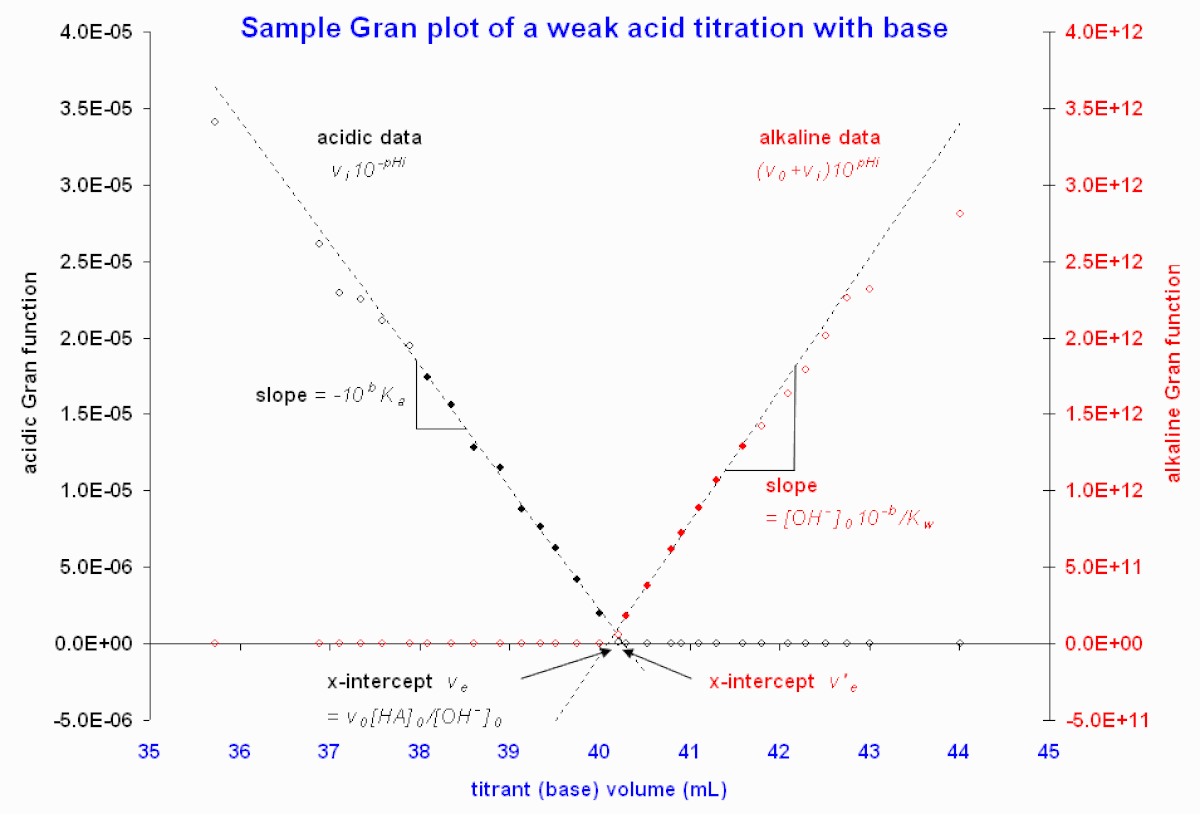
Figure 2. graphes de Gran illustratifs à partir des données d'une source en ligne. Consulté le 2008-02-18 Seule la région près de l'équivalence est présentée, puisque les données loin du point d'équivalence devient fortement de la linéarité. Les cercles emplis indiquent les points retenus pour le calcul de l'intercepte par la méthode des moindres carrées donnant les courbes pointillées.
La méthode peut estimer les constantes de dissociation d'acides faibles, ainsi que leurs concentrations (Gran, 1952). Si l'acide est representé par HA, où
-
![K_a = \frac{[H^+]_i[A^-]_i}{[HA]_i}](https://static.techno-science.net/illustration/Definitions/autres/a/ab98d889b8f6e03063ebfa77d7239869_fd8fd58cc8577a7cdb022f5f709742f9.png)
on aura à chaque ième point d'un titrage d'un volume v0 d'un acide à concentration [HA]0 par une base à concentration [OH − ]0 dans la région linéaire loin d'équivalence
-
![[HA]_i \approx \frac{v_0 [HA]_0-v_i[OH^-]_0}{v_0+v_i}](https://static.techno-science.net/illustration/Definitions/autres/1/12ad61b97d063e1f5f2ed55f1a8de914_5726b659f6042336c5271e0e3e069143.png)
-
![[A^-]_i \approx \frac{v_i[OH^-]_0}{v_0+v_i}](https://static.techno-science.net/illustration/Definitions/autres/3/32b500a948bf100b3443bc58b04303bb_9a84cdad171907f2b2415cd6de81e883.png)
qui sont des approximations valides, d'où
-
![K_a \approx \frac{10^{-pH_i} v_i[OH^-]_0}{v_0 [HA]_0-v_i[OH^-]_0}](https://static.techno-science.net/illustration/Definitions/autres/c/c7acdbbbd193a5408e54c4612a652e7c_d2451620ea0e066c0f1533a96dc326e3.png)
-
![K_a (v_0 \frac{[HA]_0}{[OH^-]_0}-v_i) \approx 10^{-pH_i} v_i](https://static.techno-science.net/illustration/Definitions/autres/1/1f8cfd22bfdffad7fe9dea10405babe6_399116f6375ab84485ea5c22d5ca670d.png)
![v_e = v_0 \frac{[HA]_0}{[OH^-]_0}](https://static.techno-science.net/illustration/Definitions/autres/5/5e3724251c9f9d62446ef04e429343f9_4402a0999b026be86455ef4bee900f45.png)
-
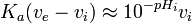
Un graphe de
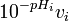
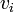
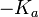
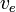
![[HA]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/4/4dac97f202ae168d52a5b3ab78b02424_21e3c3cf0d8758ee5f48b71bd57f81f7.png)
![[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/a/a6768ed3c004ea99b7818ac314e0f47c_2bc6b5bf1ee0d64d78cdeab54c7c3776.png)
Des équations semblables peuvent être dérivées pour un titrage d'une base faible par un acide fort. (Gran, 1952; Harris, 1998).
![K_{w^{ }} = [H^+]_i[OH^-]_i](https://static.techno-science.net/illustration/Definitions/autres/d/d5d8e4c93454a77e03626b65ab8d2943_64272d4f874301a1740e41d955c4d994.png)

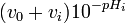
![-[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/5/5f33e1b6659cb095ee8ace58c6600f52_19032850da5f7ed5ed91bb0268651f8d.png)
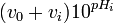
![[OH^-]_0/K_{w^{ }}](https://static.techno-science.net/illustration/Definitions/autres/9/95483d311f0fbfbdd34b5a244decd048_864fdcd4f114474cbae3462f556959f4.png)
![v_e=v_0 [H^+]_0/[OH^-]_{0^{ }}](https://static.techno-science.net/illustration/Definitions/autres/f/fa8f22bf3df8051351474ba8990a1d2d_abb8c0bafbe7e379df08f02f2a3d66d0.png)

















































