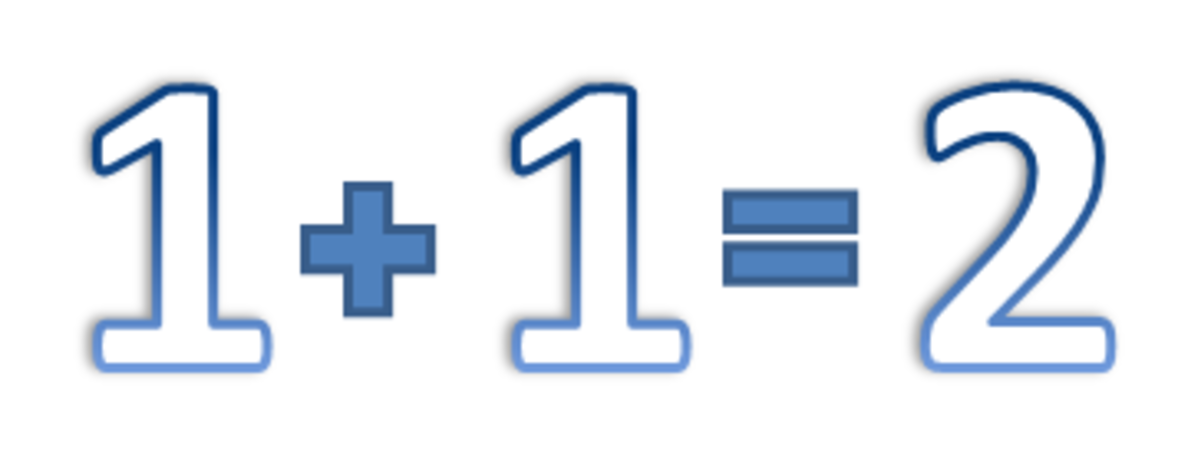Addition - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'addition est une opération élémentaire, permettant notamment de décrire la réunion de quantités ou l'adjonction de grandeurs extensives de même nature, comme les longueurs, les aires, ou les volumes. En particulier en physique, l'addition de deux grandeurs ne peut s'effectuer numériquement que si ces grandeurs sont exprimées avec la même unité de mesure. Le résultat d'une addition est appelé une somme.
En mathématiques, l'addition est développée sur les ensembles de nombres usuels mais se définit aussi pour d' comme les vecteurs et les fonctions.
Par analogie, on appelle addition la loi de composition interne des espaces vectoriels et de certains groupes abéliens. D' mathématiques sont également munies d'opérations binaires appelées additions, mais qui ne satisfont pas toujours les de l'addition usuelle.

Conception
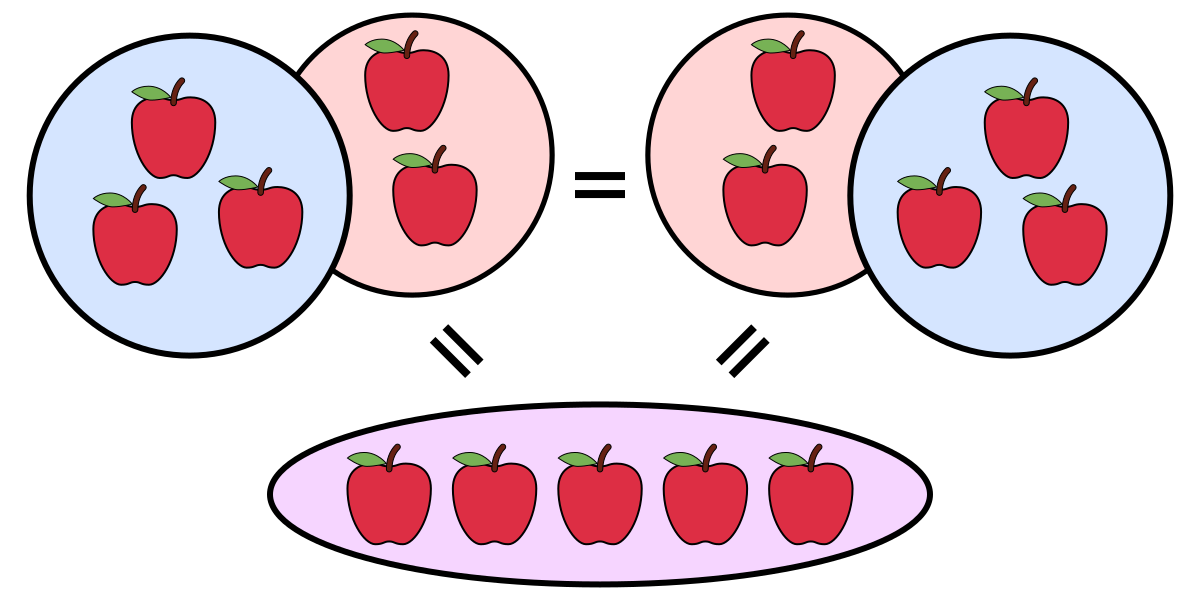
Réunion de quantités
L'addition se conçoit d'abord comme le dénombrement d'une réunion de collections d'objets, à trois conditions :
- D'une part, ces objets ne doivent pas perdre leur individualité quand on les réunit, comme le feraient des liquides ou des boules soit par un comptage, soit par un calcul mathématique sur les nombres décrivant les quantités de départ.
De même, pour que l'addition puisse décrire la réunion d'objets fractionnaires, comme des portions de cercle ou des figures géométriques tracées sur un quadrillage, il faut que tous les objets soient évalués à partir d'une sous-division commune, une brique élémentaire. Mathématiquement, cette condition s'interprète comme la recherche d'un dénominateur commun à plusieurs fractions.
Certaines grandeurs physiques, mais aussi ou économiques, peuvent également s'additionner par la réunion des objets sur lesquels elles sont mesurées. Mais ces grandeurs doivent alors être évaluées relativement à une unité de mesure commune.
Bilan de variations
L'addition peut mettre en jeu des nombres négatifs en apparaissant comme le bilan des variations ou des déplacements successifs le long d'un axe orienté. Chaque terme est alors muni d'un signe indiquant son sens : positif pour un gain, une augmentation ou un déplacement dans le sens de l'axe ; négatif pour une perte, une diminution ou un déplacement dans le sens contraire à celui de l'axe. Le résultat de l'opération est alors appelé une « somme algébrique ».
Les variations peuvent là encore concerner des quantités entières ou fractionnaires, ou n'importe quelle grandeur mesurée.
Par exemple, l'addition de − 5 et + 2 traduit une perte de cinq unités et le gain de deux unités. Le résultat de l'addition, − 3, correspond à la variation globale du nombre d'unités : trois unités ont été perdues.
Cette conception peut être étendue pour définir l' par juxtaposition de déplacements ou translations, en n'imposant plus qu'ils se fassent le long d'un même axe.
Construction formelle
La formalisation mathématique des nombres entiers naturels privilégie cependant une définition ordinale de l'addition, par récurrence. Ainsi, partant de la seule opération « ajouter un », l'addition des nombres 3 et 2 se conçoit sous la forme « 3 auquel on ajoute un par deux fois » (3+1+1). Dans ce contexte, les propriétés de commutativité et d'associativité ne sont alors plus du tout évidentes et doivent être démontrées.
À partir de l'addition des entiers naturels, sont construites successivement les additions des entiers relatifs, des rationnels, des réels et des complexes. (Cet ordre ne reflète pas l'ordre chronologique avec lequel sont apparus ces ensembles de nombres.)