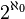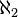Hypothèse du continu - Définition

Généralisation

L'hypothèse généralisée du continu dit qu'il n'existe pas d'ensemble dont le cardinal serait strictement compris entre et , α parcourant les ordinaux et 2^κ étant le cardinal de l'ensemble des parties d'un ensemble de cardinal κ.

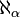
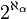
On aurait alors  : il n'y aurait rien entre un cardinal et l'ensemble de ses parties, à bijection près. Cette hypothèse, plus forte que celle du continu, est également indécidable d'après les travaux de Gödel et Cohen.

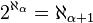
Une argumentation plausible contre l’hypothèse du continu

Bien que les travaux de Cohen mettent a priori fin au débat, il reste la possibilité de découvrir de nouveaux axiomes "plausibles" résolvant la question dans un sens ou dans l'autre. Cohen lui-même a montré que les axiomes de grands cardinaux ne peuvent à eux seuls modifier l'indécidabilité de CH, mais des travaux récents de W. Hugh Woodin laissent entendre que l'hypothèse du continu est essentiellement fausse. L'auteur a introduit une méta-logique appelée Ω-logique basée sur les ensembles projectifs. La Ω-conjecture de Woodin dit que tout énoncé essentiellement vrai dans la Ω-logique est Ω-prouvable. De sérieux indices laissent à penser que cette conjecture est vraie. En utilisant des axiomes de grands cardinaux, plus la conjecture ci-dessus, on en déduit alors que l'hypothèse du continu serait essentiellement fausse, et plus précisément que serait égal à , mais ces résultats sont loin de faire l'unanimité chez les théoriciens.