Hypothèse du continu - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition de l'hypothèse du continu - Indécidabilité - Cardinalité - Hypothèse généralisée du continu et axiome du choix - Généralisation - Une argumentation plausible contre l’hypothèse du continu

Introduction

En théorie des ensembles, l'hypothèse du continu, due à Georg Cantor, affirme qu'il n'existe aucun ensemble dont le cardinal est strictement compris entre le cardinal de l'ensemble des entiers naturels et celui de l'ensemble des nombres réels. En d'autres termes : tout ensemble strictement plus grand, au sens de la cardinalité, que l'ensemble des entiers naturels doit contenir une « copie » de l'ensemble des nombres réels. Cantor avait démontré (et publié en 1874) que le cardinal de l'ensemble des nombres réels était strictement plus grand que celui des nombres entiers, il formula plus tard cette hypothèse, qui résultait d'une analyse des sous-ensembles de la droite réelle, et de sa hiérarchisation des cardinaux infinis, mais il tenta en vain de la démontrer. Cette démonstration constituait le premier de la célèbre liste des 23 problèmes de Hilbert, que celui-ci avait établie pour le congrès international des mathématiciens de 1900 à Paris, afin de guider la recherche en mathématiques du siècle alors naissant.

Ce n'est que bien plus tard, en 1963, que Paul Cohen introduisit sa méthode de forcing pour montrer que cette hypothèse ne pouvait se déduire des axiomes de la théorie des ensembles ZFC, généralement considérée comme une formalisation adéquate de la théorie des ensembles de Cantor, qui n'était pas encore axiomatisée en 1900. Kurt Gödel avait précédemment démontré, en 1938, que cette hypothèse n'était pas non plus réfutable dans ZFC. Elle est donc indépendante des axiomes de la théorie des ensembles ZFC, ou encore indécidable dans cette théorie.

La méthode du forcing de Cohen a connu depuis de nombreux développements en théorie des ensembles. Son résultat n'a pas mis un point final aux travaux sur le sujet. La recherche d'hypothèses naturelles à ajouter à la théorie ZFC et d'arguments qui permettraient de trancher pour ou contre l'hypothèse du continu constitue toujours un sujet actif en théorie des ensembles.

Définition de l'hypothèse du continu

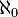
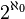
On définit $\aleph_0$ (aleph zéro) comme le cardinal de $\mathbb{N}$ . Le cardinal de $\mathbb{R}$ est noté usuellement $2^{\aleph_0}$ .
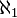
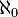
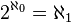
Soit $\aleph_1$ le plus petit cardinal strictement supérieur à $\aleph_0$ , l'hypothèse du continu déclare que $2^{\aleph_0} = \aleph_1$ . En d'autres termes, cela signifie qu'il n'existe pas d'ensemble infini dont le cardinal serait strictement compris entre le cardinal de $\mathbb{N}$ et celui de $\mathbb{R}$ . On passe donc du dénombrable (ou discret), au continu, en faisant un seul bond.

Indécidabilité

Kurt Gödel a montré en 1938 que l'ajout de l'hypothèse du continu à la théorie des ensembles, définie par exemple par les axiomes de Zermelo-Fraenkel, ne changeait nullement la consistance de cette théorie, même si on l'augmente de l'axiome du choix.

Paul Cohen a montré en 1963 que l'hypothèse du continu n'était pas démontrable dans la théorie des ensembles basée sur les axiomes de Zermelo-Fraenkel. Elle est donc indépendante de la théorie des ensembles.

Commencée il y a une trentaine d'années, la recherche d'axiomes « naturels » à ajouter à la théorie de Zermelo-Fraenkel (axiome de détermination, axiomes de grands cardinaux etc.) va peut-être permettre, grâce aux travaux de W. Hugh Woodin, de résoudre prochainement l'hypothèse du continu... par la négative (voir ci-dessous), ce que soupçonnait déjà Gödel.

Il n'y a pas de quoi être surpris de l'existence d'énoncés ne pouvant être démontrés ou infirmés à partir d'un système d'axiomes donné, c'est par exemple le cas du postulat d'Euclide relativement à son système « axiomatique ».

L'hypothèse du continu n'est pas sans rapport avec des énoncés d'analyse, ou de théorie de la mesure.

Historiquement, les mathématiciens en faveur d'une large classe d'ensembles rejettent l'hypothèse du continu, alors que ceux favorables au contraire à une ontologie ensembliste plus restreinte l'acceptent.