Nombre hyperréel - Définition

Historique

Les nombres hyperréels furent introduits par Abraham Robinson dans les années 1960 dans le cadre de ses travaux sur l'analyse non standard. Robinson rejoignait les préoccupations d'Euler (et des autres analystes du XVIII^e siècle) cherchant à donner un sens aux nombres infiniment grands et infiniment petits. La construction de Robinson utilisait essentiellement la théorie des modèles. Une construction plus explicite à l'aide d'ultraproduits fut découverte quelques années plus tard, et c'est celle qui va être exposée ici. Par la suite, une approche axiomatique plus générale de l'analyse non standard, la théorie des ensembles internes (Internal Set Theory, ou IST), fut proposée par Edward Nelson : elle se base sur l'axiomatique de Zermelo-Fraenkel à laquelle sont ajoutés trois axiomes nouveaux ; la description détaillée de ces axiomes et de leurs conséquences est donnée dans l'article : analyse non standard. Dans cette dernière approche (qui a d'ailleurs des applications beaucoup plus générales que la construction d'infinitésimaux), on ne crée pas à proprement parler de nouveaux réels, mais on distingue parmi les réels une collection (qui n'est pas un ensemble) de réels standards, les autres se comportant par rapport à ceux-ci comme des infiniment petits ou des infiniment grands par exemple.

Un exemple d'utilisation

Avec les définitions précédentes, beaucoup de notions de l'analyse classique s'expriment de manière plus simple : ainsi, si est un infinitésimal non nul, la dérivée de f en a est l'ombre de l'hyperréel  : tout se passe comme si on n'avait plus besoin de la notion de limite. On trouvera d'autres exemples (et des précisions sur la validité de ces raisonnements) dans l'article analyse non standard.

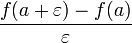
Définitions

Un nombre hyperréel x est dit

• infinitésimal, si |x| est strictement inférieur à tout réel positif

• infiniment grand si 1/x est infinitésimal.

• appréciable s'il n'est ni infiniment petit, ni infiniment grand.

Pour tout x appréciable, il existe un réel unique, la partie standard (ou l'ombre) de x (noté x*) tel que x-x* soit infinitésimal ; l'écriture en x*+ε de tout nombre hyperréel non infiniment grand provient d'une simple dichotomie (dans R) autorisée par l'ordre total sur . En effet un nombre hyperréel non infiniment grand est contenu dans un segment à bornes réelles ; on coupe successivement ce segment en 2 pour encadrer le nombre hyperréel de plus en plus précisément. Par le théorème des segments emboîtés, on obtient ainsi le nombre réel unique x*.